翻译自论文 “Core Transform Design in the High Efficiency Video Coding (HEVC) Standard”
A. Use of Transforms in Block-Based Video Coding
在基于块的混合视频编码方法中,变换应用于帧间或帧内预测产生的残差信号,如图 1 所示。在编码器处,帧的残差信号被划分大小为\(N×N\)的方形块, 其中\(N=2^M\)和M是一个整数。 然后将每个残差块 (\(U\)) 输入到二维\(N×N\)正向变换。 通过分别对每行和每列应用\(N\)点一维变换,可以将二维变换实现为可分离变换。 然后对得到的变换系数(\(coeff\))进行量化(相当于除以量化步长\(Q_{step}\))以获得量化变换系数(\(level\))。 在解码器处,量化的变换系数随后被反量化(这相当于乘以\(Q_{step}\))。 最后,将二维可分离逆变换应用于反量化变换系数(\(coeff_Q\)),从而产生量化样本的残余块,然后将其添加到帧内或帧间预测样本以获得重建块。

通常,正向变换矩阵和逆变换矩阵是彼此转置的,并且被设计为在没有中间量化和去量化步骤的情况下连接时实现输入残差块的近乎无损重建。
在 HEVC 等视频编码标准中,指定了反量化过程和逆变换,而正向变换和量化过程则由实施者选择(受到比特流的约束)。 然而,在下文中,除非另有说明,我们将根据正向变换矩阵讨论 HEVC 核心变换的设计和属性。 逆变换在HEVC标准中被指定为对应的转置矩阵。
B. Discrete Cosine Transform
应用于输入样本\(u_i\)的\(N\)点 1D DCT 的变换系数\(w_i\)可以表示为:
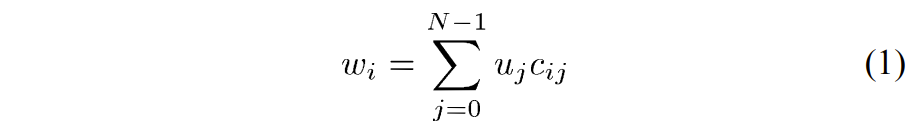
这里\(i=0,…,N-1\),\(c_{ij}\)为DCT变换矩阵\(C\)的系数,定义如下:
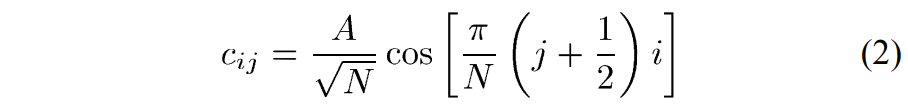
这里\(i,j=0,…,N-1\), \(A = 1\) or \(2^{1/2}\) for \( i = 0 \) or \(i > 0\),DCT的基向量\(c_i\)定义为\(c_i=[c_{i0},…,c_{i(N-1)}]^T, i=0,…,N-1\)
DCT 具有多个被认为对于压缩效率和高效实现都有用的属性:
- 基向量是正交的,即\(c^T_ic_j=0\)。 该属性对于通过实现不相关的变换系数来提高压缩效率是理想的。
- DCT 的基向量已被证明可以提供良好的能量压缩,这对于压缩效率来说也是理想的。
- DCT 的基向量具有相等的范数,即\(c^T_ic_i=1\)。 该属性对于简化量化/去量化过程是有利的。 假设需要量化误差的相等频率加权,则基向量的相等范数消除了对量化/去量化矩阵的需要。
- 让\(N=2^M\)。 大小为\(2^M×2^M\) DCT 矩阵的元素是 \(2^{(M+1)}×2^{(M+1)}\) DCT 矩阵元素的子集。更具体地,较小矩阵的基向量等于较大矩阵的偶数基向量的前半部分。 此属性对于降低实施成本很有用,因为相同的乘法器可以重复用于各种变换大小。
- DCT矩阵可以通过使用少量的唯一元素来指定。 通过检查 (2) 的元素\(c_{ij}\),可以看出大小为 \(2^M×2^M\)的 DCT 矩阵中唯一元素的数量等于 \(2^M-1\)。
- DCT的偶数基向量是对称的,而奇数基向量是反对称的。 此属性对于减少算术运算的数量很有用。
- DCT 矩阵的系数具有一定的三角关系,可以减少算术运算的数量,超出利用(反对)对称性质所能实现的数量。
C. Finite Precision DCT Approximations
HEVC 的核心变换矩阵是 DCT 矩阵的有限精度近似。 在视频编码标准中使用有限精度的好处是,实值 DCT 矩阵的近似值在标准中指定,而不是依赖于实现。 这可以避免制造商使用略有不同的浮点表示实现 IDCT 所导致的编码器-解码器不匹配。 另一方面,使用近似矩阵元素的缺点是第 B 节中讨论的 DCT 的一些属性可能不再满足。 更具体地说,在与对矩阵元素使用高位深度相关的计算成本和满足第 B 节的一些条件的程度之间存在权衡。
确定 DCT 矩阵元素的整数近似值的一种直接方法是用某个大数(通常在\(2^5\)和\(2^{16}\)之间)缩放每个矩阵元素,然后舍入到最接近的整数。 然而,这种方法并不一定能产生最佳的压缩性能。 如第 D 节所示,对于给定的矩阵元素位深度,近似 DCT 矩阵元素的不同策略会导致第 B 节的一些属性之间的不同权衡。
D. HEVC Core Transform Design Principles
用于 HEVC 核心变换的 DCT 近似是根据以下原则选择的。 首先,B 部分的属性 4、5 和 6 得到满足,没有任何妥协。 这种选择确保了 DCT 的几个实现友好的方面得以保留。 其次,对于属性 1、2、3 和 7,在用于表示每个矩阵元素的位数和满足每个属性的程度之间存在权衡。
为了测量属性 1、2 和 3 的近似程度,为整数点 DCT 近似定义了以下测量,其缩放矩阵元素等于\(d_{ij}\),基向量\(d_i=[d_{i0},…,d_{i(N-1)}]^T, i=0,…,N-1\)
- 正交性度量:\(o_{ij}=d^T_id_j/d^T_0d_0, i≠j\)
- 与 DCT 的相似性度量:\(m_{ij}=|αc_{ij}-d_{ij}|/d_{00}\)
- 范数度量:\(n_i=|1-d^T_id_j/d^T_0d_0|\)
比例因子\(α\)定义为 \(d_{00}N^{1/2}\)。
经过仔细研究,决定用8位(包括符号位)来表示每个矩阵系数,并选择第一基向量的元素等于64(即 ,\(d_{0j}=64\))。 请注意,与正交 DCT 相比,这会导致 HEVC 变换矩阵的比例因子为\(2^{(6+M/2)}\)。 其余矩阵元素进行手动调整(在属性 4、5 和 6 的约束内),以实现属性 1、2 和 3 之间的良好平衡。手动调整执行如下。 首先,推导出实值缩放 DCT 矩阵元素\(αc_{ij}\) 。
接下来,对于结果矩阵中的每个唯一数字,检查\(αc_{ij}\)区间 [-1.5, 1.5] 周围的每个整数值,并计算 \(o_{ij}\)、 \(m_{ij}\)和 \(n_{ij}\)值。 由于变换矩阵中只有 31 个唯一数字(参见第 E 节),因此可以系统地检查各种排列(尽管不是详尽的)。 选择最终的整数矩阵元素是为了在所有测量 \(o_{ij}\)、 \(m_{ij}\)和 \(n_{ij}\)之间提供良好的折衷。 所得到\(o_{ij}\)、 \(m_{ij}\)和 \(n_{ij}\)的最坏情况值显示在表 I 的第二列中。范数被认为足够接近 1(即范数测量\(n_{ij}\)足够接近 0),以证明不使用非平坦默认值是合理的 HEVC 中的去量化矩阵(即所有变换系数均等缩放)。

为了比较的目的,表I的第三列中列出了将实值DCT矩阵元素与\(2^{(6+M/2)}\)相乘并舍入到最接近的整数时的结果测量。从表中可以看出,虽然HEVC变换的矩阵元素距离缩放后的DCT矩阵元素较远,但它们具有更好的正交性和范数性质。
最后,仅使用 8 位表示,B 节的属性 7(矩阵元素之间的三角关系)不容易保留。 作者不知道 HEVC 核心变换的任何三角特性可用于将算术运算数量减少到低于使用(反)对称特性时所需的数量。
E. Basis Vectors of the HEVC Core Transforms
指定32点正向变换的32×32矩阵的左半部分如图2所示。
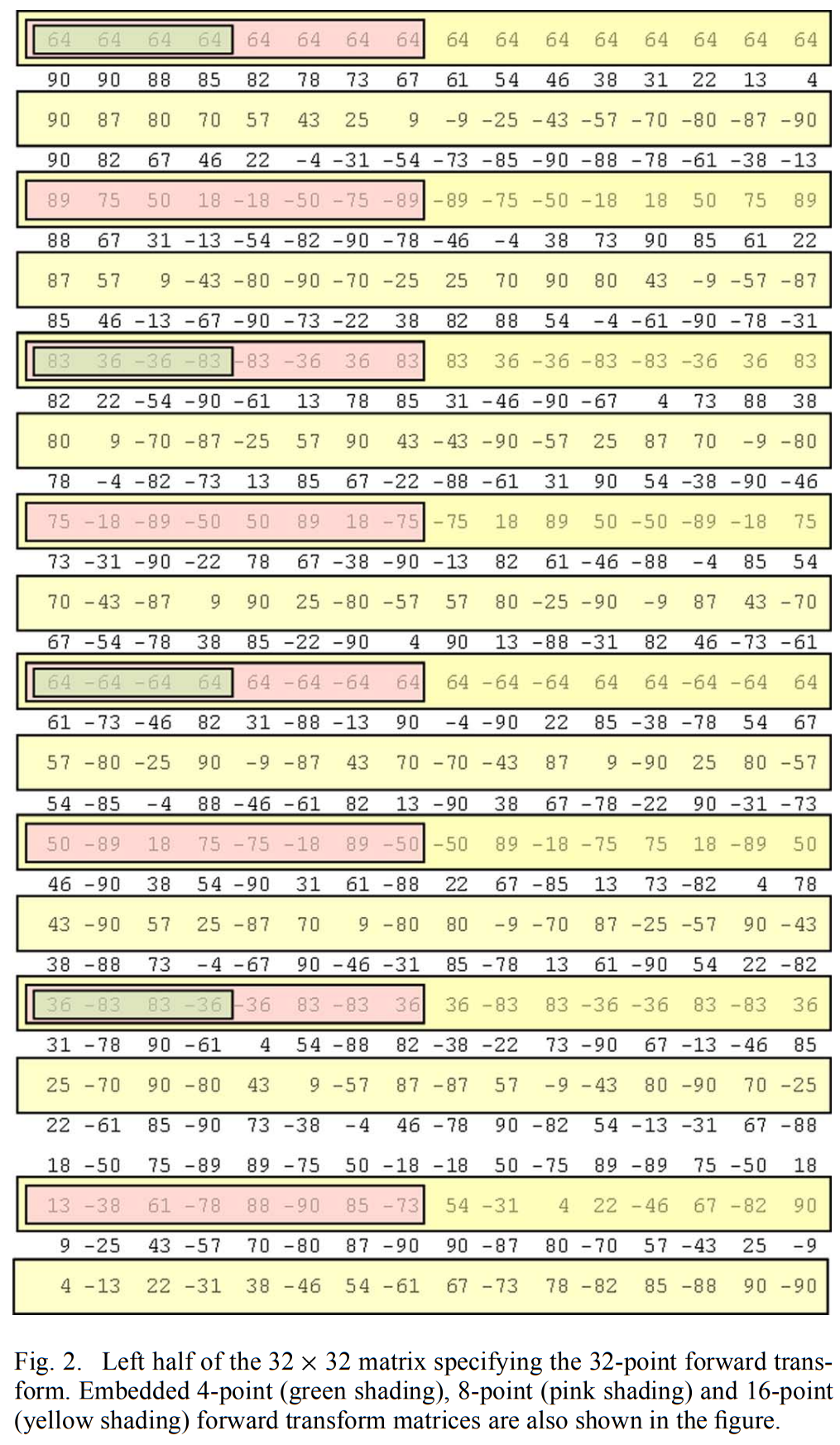
右半部分可以通过使用基向量的(反)对称性质(B节的性质6)来导出。HEVC的逆变换矩阵被定义为图中矩阵的转置。32×32矩阵包含多达31个唯一数字,如下所示:

这些唯一数字是正向变换矩阵的第一列的元素1至31。请注意,尽管数字90出现了三次,但这是偶然的,通常不是真的。
此外,较小变换矩阵\(N=4,8,16\)的系数可以从 32×32 变换矩阵的系数导出为:
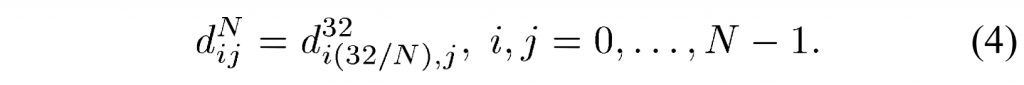
让\(D_4\)表示 4×4 变换矩阵。 利用式(4)和图2,\(D_4\)可得:
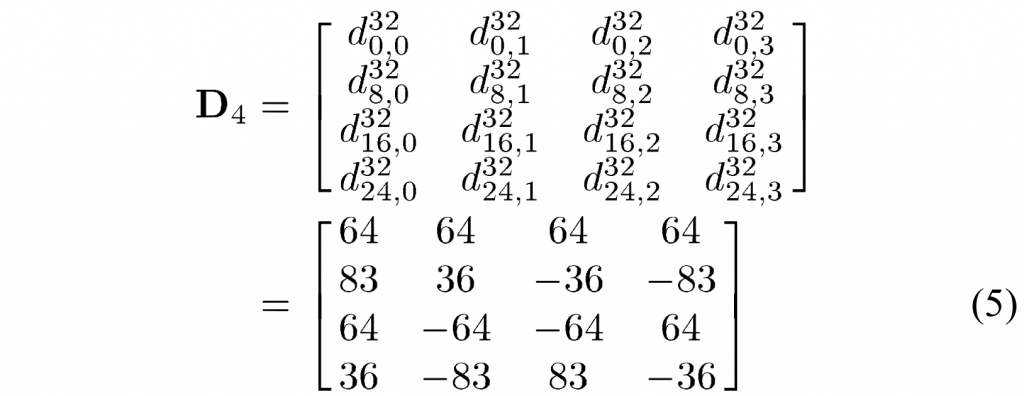
8×8 变换矩阵和16×16 变换矩阵可以类似地从32×32 变换矩阵获得,如图2所示,其中使用不同的颜色来突出显示嵌入的16×16、8×8 和4×4 正向变换矩阵。 此属性允许使用相同的架构来实现不同的变换大小,从而促进不同变换大小之间的硬件共享。
请注意,根据 (3) 的唯一数属性和(反对)对称属性,\(D_4\)也等于:
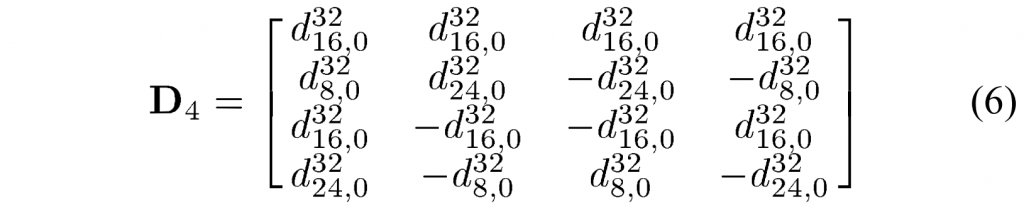
F. Intermediate Scaling
由于与正交DCT变换相比,HEVC矩阵是按比例\(2^{(6+M/2)}\)缩放的,并且为了通过正向和反向二维变换保持残差块的范数,需要应用额外的比例因子\(S_{T1}\)、\(S_{T2}\)、\(S_{IT1}\)、\(S_{IT2}\),如图3所示。请注意,图3基本上是图1中变换和量化的定点实现。虽然HEVC标准规定了逆变换的比例因子(即\(S_{IT1}\)、\(S_{IT2}\)),但HEVC参考软件也规定了前向变换的相应比例因子(例如\(S_{T1}\)、\(S_{T2}\))。比例因子是在以下限制条件下选择的:
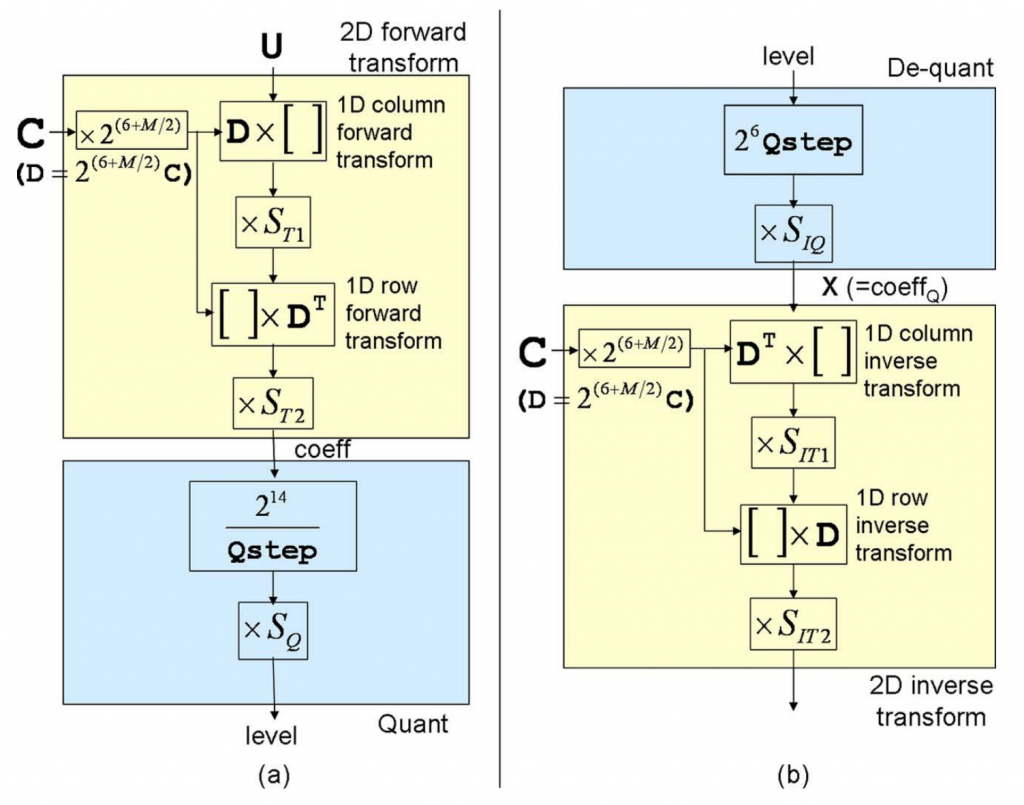
- 所有缩放因子应为 2 的幂,以允许缩放以右移的方式实现。
- 假设输入残差块的全范围(例如,所有样本都具有最大幅度的DC块),每个变换阶段之后的位深度应等于16位(包括符号位)。 这被认为是准确性和实施成本之间的合理权衡。
- 由于HEVC矩阵按比例\(2^{(6+M/2)}\)缩放,2D正向变换和逆变换的级联将导致1D行正向变换、1D列正向变换、1D列逆变换和1D行逆变换中的每一个的按比例\(2^{(6+M/2)}\)缩放。因此,为了通过二维正变换和逆变换保持范数,所有比例因子的乘积应等于\((1/2^{(6+M/2)})^4=2^{-24}2^{-2M}\)。
图4以4×4正向变换为例说明了选择正向变换比例因子的过程。当视频具有B bit位深度时,残差将在需要(B+1)位来表示的范围\([-2^B+1,2^B-1]\)内。 在下面的worst case 位深度分析中,我们将假设残差块的所有样本的最大振幅等于正向变换第一阶段的输入。 我们相信这是一个合理的假设,因为所有基向量都具有几乎相同的范数。
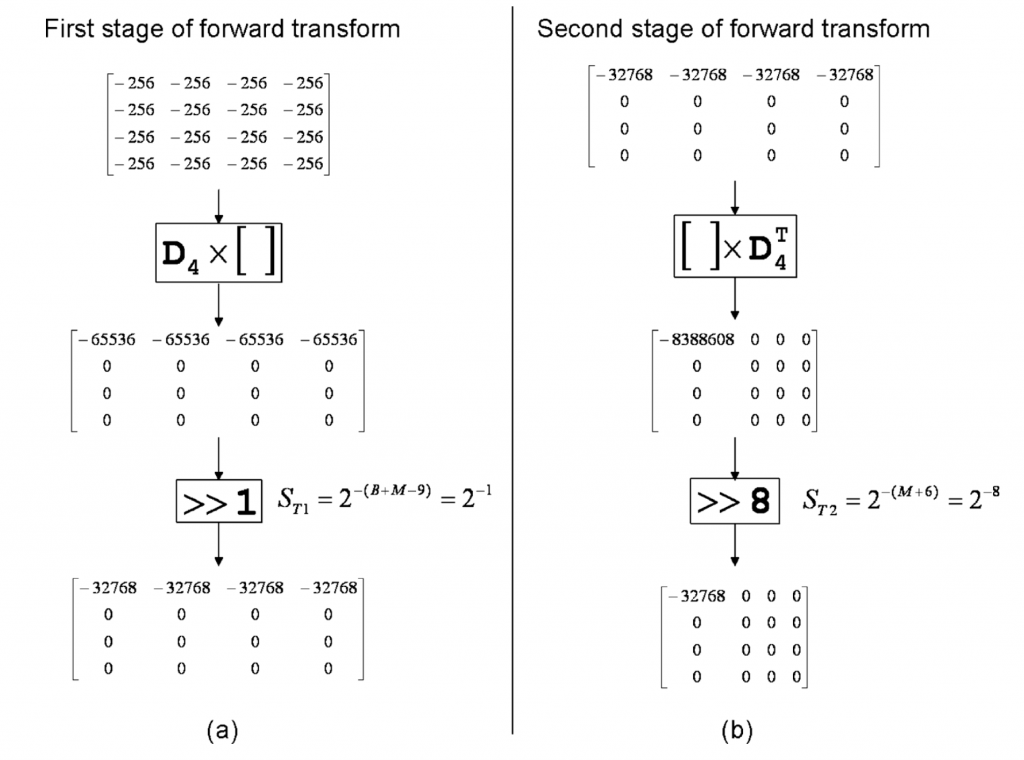
还要注意,在worst case 分析中,我们使用\(-2^B\)而不是\(-2^B+1\)或\(2^B-1\),因为它是2的幂。由于所有比例因子都是2的幂,所以假设输入为\(-2^B\)(仍然适合(B+1)位),则比例因子推导变得更简单。对于这种worst case的输入块,输出样本的最大值将为\(-2^B×N×64\)。这对应于第一基向量(长度为N,所有值均等于64)与由等于\(-2^B\)的值组成的输入向量的点积。因此,对于\(N=2^M\),为了使输出适合于16位(即,\(2^{-15}\)的最大值)内,需要\(1/(2^B×2^M×2^6×2^{-15})\)的缩放。因此,第一变换阶段之后的比例因子被选择为\(S_{T1}=2^{-(B+M-9)}\)。
正向变换的第二阶段由第一变换阶段的结果与\(D^T_4\)相乘组成。正向变换第二阶段的输入是第一阶段的输出,该输出是一个矩阵,第一行中的所有元素都具有 \(2^{-15}\)的值。所有其他元素将为零,如图 4(b) 所示。 与\(D^T_4\)相乘的输出将是一个矩阵,其中仅 DC 值等于 \(2^M×2^6×2^{-15}\),所有其余值等于 0。这意味着第二阶段变换后所需的缩放为 \(S_{T2}=2^{-(M+6)}\),以便输出适合 16 位。
逆变换的第一阶段由正变换的结果与\(D^T_4\)相乘组成。逆变换第一阶段的输入是正变换的输出矩阵,该矩阵是仅 DC 元素等于\(2^{-15}\)的矩阵。 与\(D^T_4\)相乘的输出将是一个矩阵,其第一列元素等于 \(2^6×2^{-15}\)。因此,在逆变换的第一阶段之后,为了使输出适合 16 位,所需的缩放是\(S_{IT1}=2^{-6}\)。
逆变换的第二阶段包括将逆变换的第一阶段的结果与\(D_4\)相乘。 逆变换第二级的输入是逆变换第一级的输出矩阵,该矩阵的第一列元素等于\(2^{-15}\)。与\(D_4\)相乘的输出将是所有元素等于\(2^6×2^{-15}\)的矩阵。 因此,在第二阶段逆变换之后,为了使输出值进入 \([-2^B,2^B-1]\)的原始范围所需的缩放是 \(S_{IT1}=2^{-21-B}\)。
总之,本节中施加的约束会在不同的变换阶段后产生以下比例因子:
- 在第一个正向变换阶段之后:\(S_{T1}=2^{-(B+M-9)}\)
- 在第二个正向变换阶段之后:\(S_{T2}=2^{-(M+6)}\)
- 在第一个逆变换阶段之后:\(S_{IT1}=2^{-6}\)
- 在第二个逆变换阶段之后:\(S_{IT1}=2^{-21-B}\)
其中B是输入/输出信号的位深度(例如 8 位), 是\(M=log2(N)\)。
在没有量化/去量化的情况下,比例因子的这种选择可确保在所有变换阶段之后的位深度为 16 位。 然而,量化/反量化过程引入的量化误差可能会将每个逆变换阶段之前的动态范围增加到超过 16 位。 例如,考虑 B = 8 和正向变换的所有输入样本等于 255 的情况。在这种情况下,正向变换的输出将是值等于 \(255<<7 =32640\) 的 DC 系数。对于高 QP 值并使用向上舍入量化器,每个逆变换级的输入很容易超出 [-32768, 32767] 允许的 16 位动态范围。 虽然在去量化器之后clip到 16 位范围被认为是微不足道的,但在第一个逆变换阶段之后被认为是不受欢迎的。 为了允许一定程度的量化误差,同时将两个逆变换级之间的动态范围限制为 16 位,逆变换比例因子的选择最终修改如下:
- 在第一个逆变换阶段之后:\(S_{IT1}=2^{-7}\)
- 在第二个逆变换阶段之后:\(S_{IT1}=2^{-20-B}\)
逆变换比例因子的使用如图 5 所示,以 4×4 逆变换为例,假设输入是图 4 的最终输出。
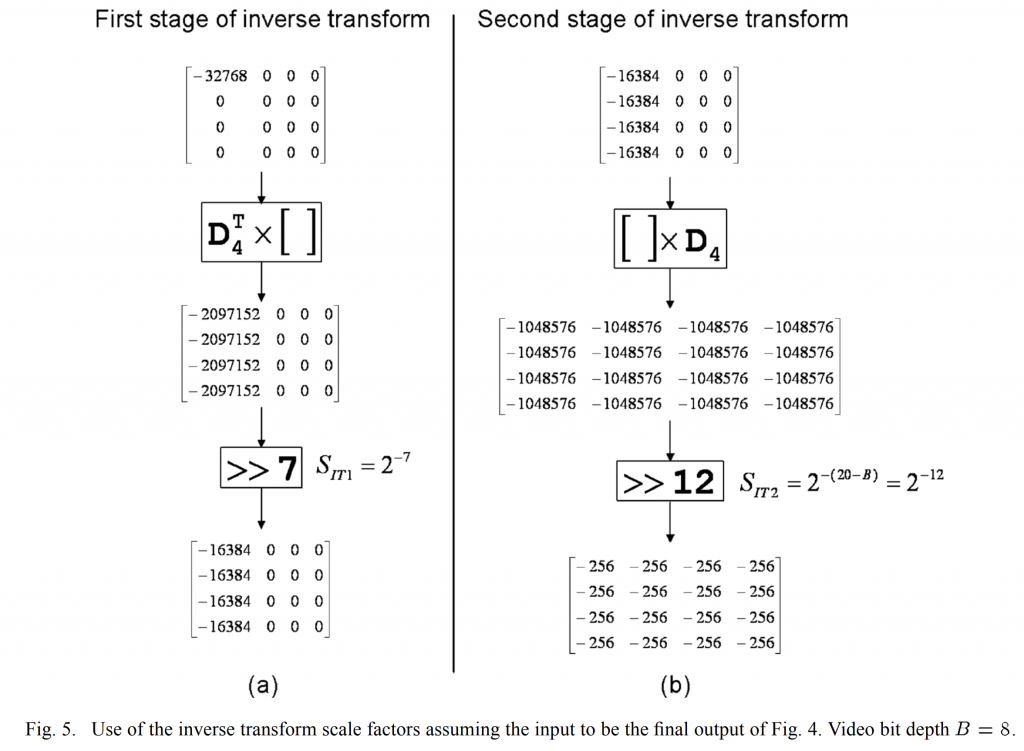
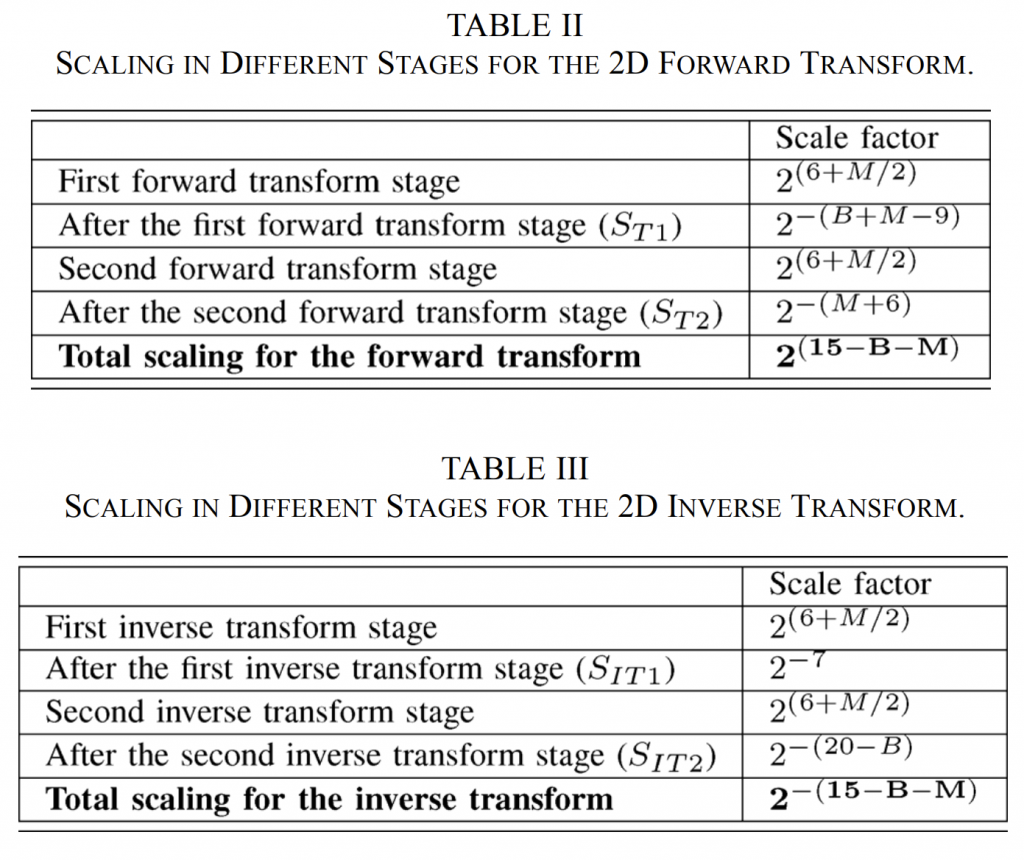
表 II 和表 III 分别总结了与正交 DCT 相比正向变换和反向变换的不同缩放因子。
HEVC规范指定在缩放之前添加的偏移值以进行舍入。 该偏移值等于比例因子除以 2。图 3-5 中未明确显示该偏移。
最后,使用 8 位系数并将中间数据的位深度限制为 16 位的两个有用结果是,所有乘法都可以用具有 16 位或更少的乘法器来表示,并且右移之前的累加器可以用更少的位来实现。 所有变换阶段都超过 32 位。
G. Quantization and De-Quantization
量化由除以量化步长(\(Q_{step}\))组成,逆量化由乘以量化步长组成。类似于H.264/AVC,量化参数(QP)用于确定HEVC中的量化步长。可以取从0到51的52个值。1的增加意味着量化步长增加了大约12%(即\(2^{1/6}\))。增加6导致量化步长增加2倍。除了指定两个连续QP值的步长之间的相对差之外,还需要定义与QP值的范围相关联的绝对步长。这是通过为\(Q_{step}=1\)选择QP=4来完成的。
正交变换的等效量化步长之间的结果关系现在由下式给出:

式(7)也可表示为:
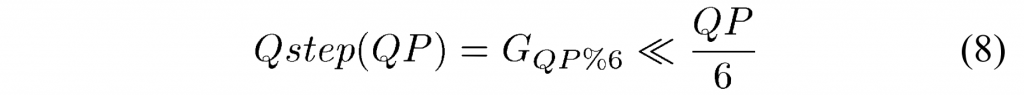

HEVC 量化和反量化基本上是(8)的定点近似。 如图 3 所示,引入了额外的比例因子 \(S_Q\)和 \(S_{IQ}\),以恢复残差块的范数,该范数由于(8)的定点实现中使用的缩放而被修改。
HEVC 中 (8) 的定点近似由下式给出:
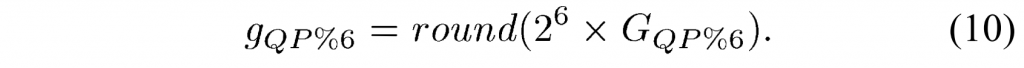
这导致
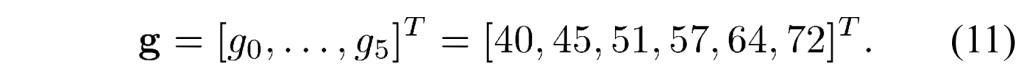
对于量化器输出、level,去量化器在 HEVC 标准中指定为:
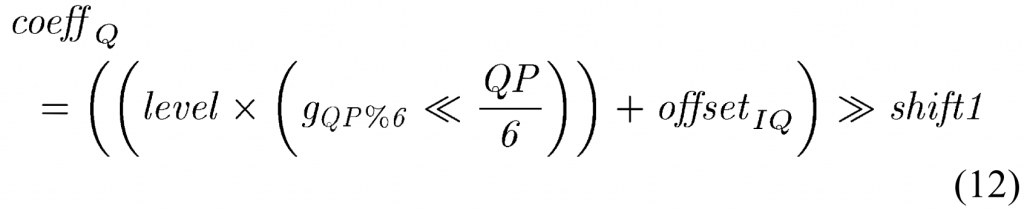
这里\(shift1=(M-9+B)\), \(offset_{IQ}=1<<(M-10+B)\).
图3的比例因子\(S_{IQ}\)等于\(2^{-shift1}\),如下所示:当QP=4时,图3中的逆变换和反量化的组合比例在相乘时应产生1的乘积,以通过逆变换和逆量化保持残差块的范数,即
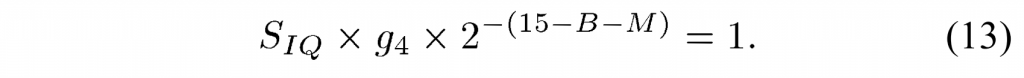
这导致\(S_{IQ}=2^{-(M-9+B)}\)导致\(shift1\)等于右移 \((M-9+B)\) 。 (13) 中的比例因子 D 从表 III 中获得。
对于正向变换的输出样本, coeff,可以按如下方式实现简单的量化方案:
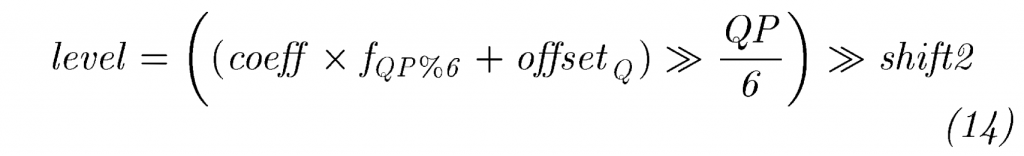
这里\(shift2=29-M-B\),
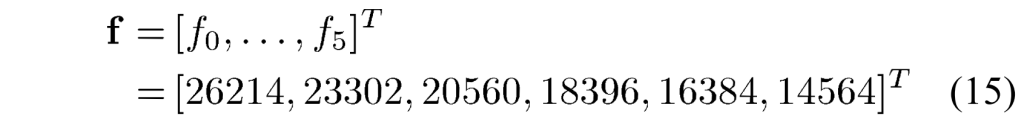
注意 \(f_{QP\%6} \approx 2^{14}/G_{QP\%6}\)。shift2的值是通过对正向变换和量化器中的组合缩放施加类似的约束来获得的,如(13)中,即 \(S_Q×f_4×2^{(15-B-M)}=1\),这里\(S_Q=2^{-shift2}\).
最后,选择 \(offset_Q\)来实现所需的舍入。
总而言之,选择量化器乘法器\(f_i\)和去量化器乘法器\(g_i\)以满足以下条件
1) 确保\(g_i\)可以用有符号的 8 位数据类型表示。
2) 确保步长从一个QP值到下一个QP值的增加几乎相等(大约 12%)
3) 通过量化和反量化过程确保近似单位增益
4) 为QP=4提供所需的量化步长绝对值。
《HEVC Core Transform Design》有一个想法