在HEVC中,对于每个变换单元,量化的变换系数以16个系数的组进行熵编码。在sign-hiding 的情况下,对于满足一定条件的系数组,沿扫描路径的第一非零系数的符号不在比特流中显式传输,而是从解码器处该系数组中的所有非零系数之和的奇偶性来推断。为了保证隐藏符号与所有非零系数之和的奇偶性匹配,编码器采用了基于率失真优化或失真最小化的奇偶性调整方法。
1 隐藏符号位的基本原理
在视频编码中,数据隐藏是一种已知的技术,通常用于将一个语法元素隐藏到部分比特流中以提供更好的编码效率。例如,用于帧内预测的MPM索引嵌入量化系数之和的奇偶性中;使用量化系数的奇偶性来传送变换模式的信息。
在将语法元素隐藏到其他语法元素的特定特征中时,必须考虑要隐藏哪个语法元素(源信号)以及要将其隐藏到哪里(目标信号)。为了产生率失真增益,必须考虑几个标准。
首先,从因果关系的角度来看,隐藏必须是可行的。在编码期间,当编码目标信号时源信号必须可用,在解码期间,必须在实际使用源信号之前解码目标信号。
其次,源信号必须代表压缩比特流中不可忽略的部分。从先前关于压缩数据隐藏的研究可知,隐藏数据时可以获得净增益,然而,以速率增益度量,它将仅表示隐藏信号的总速率的一部分。因此,如果数据隐藏要产生任何有价值的增益,则源信号应代表压缩比特流的相当大的比例。
此外,如果用于嵌入信息的目标和源信号特征不相关,则为了从隐藏源信号中获得最大增益,必须考虑其分布条件。当将二进制元素隐藏到目标信号的二进制函数中(例如将位隐藏到奇偶校验中)时,在大约50%的情况下,目标信号将需要改变。因此,由这种变化引起的率失真损失是近似恒定的,并且与源信号的分布无关:例如,隐藏始终等于0的二进制语法元素会导致相同的损失,因为奇偶校验仍然必须改变一半的时间。另一方面,当源信号在比特流中编码时达到其每符号1比特(在二进制元素的情况下)的编码上限时,通过省略源信号的传输而获得的增益是最大的。因此,必须为源信号选择一个等概率语法元素。
目标信号的一个重要条件在于能够找到对率失真性能影响最小的变化,因为在大约一半的情况下需要进行变化。因此,最好使用较大的目标信号,从而增加发现这种变化的机会。例如,将二元元素隐藏到单个量化系数的奇偶性中将在需要改变该系数时产生高率失真损失,当将其隐藏在较大的量化系数集合的和的奇偶性中时,增加了找到非常接近其量化区间边界并且其中量化值的改变将导致中等率失真损失的量化系数的机会。
最后,希望源信号和目标信号大致成比例:当有更多的数据要隐藏时,应该有更多的目标信号嵌入其中。
量化系数可以做sign-hiding的原因:
- 在编码器中,当要隐藏的符号已知时,可以修改量化系数的电平,并且在解码器中,在符号比特实际用于解码信号之前,可以使用这些电平。
- 符号位代表压缩比特流的很大一部分(在HEVC通用测试条件下为15%到20%)。
- 符号位是等概率的。
- 在一组量化系数中嵌入符号位可以提供足够的机会找到一个量化系数,该量化系数在修改时会导致中等的率失真损失。
- 当有更多的符号位要隐藏(源信号)时,有更多的剩余数据(目标信号)要嵌入它们。
2 量化和系数编码
可参考文章:
率失真优化量化 (Rate-Distortion Optimized Quantization RDOQ) – 我受到了惊吓 (mmedia-t.cn)
3 Sign Hiding
3.1 在解码器处推断隐藏符号位
对于每个CG,解码器统计沿扫描路径的第一个非零系数和最后一个非零系数之间的系数数目,并将其与阈值进行比较。如果超过阈值,则从所有非零系数之和的奇偶性推断第一个非零系数的符号。特别地,如果和为偶数,则该符号被推断为正;如果和为奇数,则该符号被推断为负。在这种情况下,不需要为该系数显式传输符号位。否则,以常规方式(每个符号1位)从比特流解码符号位。稍后在讨论编码器侧奇偶校验调整方案时,将详细说明应用这种标准以排除某些CG应用符号隐藏技术的原因。
上述多个符号位隐藏的解码处理针对一个TU内的每个CG重复。由于每个CG具有16个系数,因此对于一个4×4、8×8、16×16或32×32 TU,可分别隐藏多达1、4、16或32个符号位。
3.2 编码器中隐藏符号位
为了避免失配,编码器执行与解码器相同的检查,以比较具有相同阈值的每个CG的第一非零系数和沿扫描过程的最后非零系数之间的系数数目,以确定是否要编码第一非零系数的符号。如果该数字不大于预定义阈值,则以常规方式编码符号;否则,不显式传输第一个非零系数的符号,因此每CG节省一位。注意,所有非零系数之和的奇偶性并不总是与第一个非零系数的符号匹配。当发生这种情况时,调整量化系数的幅度,以便奇偶性匹配符号。
将一个系数组中的原始变换系数表示为\(c={c_0, c_1, … , c_{N-1}}\),其中N是系数组中的系数总数。将量化和去量化函数分别表示为\(Q(·)\)和\(Q^{-1}(·)\)。量化输出或量化变换系数表示为\(u=Q(c)={u_0, u_1, … , u_{N-1}}\)。设k是沿扫描路径的第一个非零系数的索引,即\(u_k≠0\)且\(u_i=0, 0≤i<k\)。为了优化奇偶调整后的率失真性能,可将多符号位隐藏方案表述为以下优化问题:
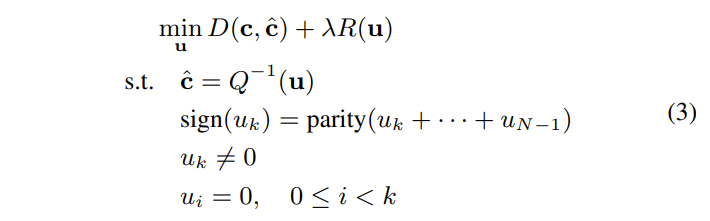
\(D(c, \hat{c})\)是c与其重构\(\hat{c}\)之间的均方失真,\(R(u)\)表示编码系数向量u所需的速率,sign(x)是符号函数,λ是拉格朗日乘子,表征了距离和编码速率之间的折衷,以及
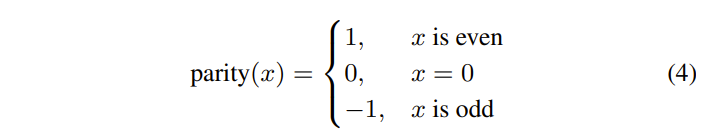
等式(3)中的问题本质上是矢量量化问题,对于该问题,需要设计矢量量化器以使给定速率约束以及和约束的奇偶性的失真最小化。因此可以应用一般的矢量量化器设计方法,然而通常需要迭代方法并且具有高设计复杂度。
在HEVC参考编码器中,当分别使用RDOQ或HDQ时,采用两种非迭代奇偶调整方案来解决等式(3)中的问题。首先通过RDOQ或HDQ对变换系数进行量化。在和的奇偶性与要隐藏的符号不匹配的情况下,编码器执行线性搜索,并将量化系数之一的幅度调整+1或-1,以使调整后的系数之和的奇偶校验与符号匹配。
第一个奇偶校验调整方案遵循与RDOQ类似的原则,即选择系数和调整方向以最小化调整后的总体率失真代价。第二种方案在不需要准确率信息的情况下,仅使失真最小化,适用于HDQ,且不太复杂。