编码标准-香不菇

VVC中的collocated picture

collocated picture 是参考帧列表中先前已编码的帧。在VVC中，每一帧的picture header中通过 ph_collocated_from_l0_flag 和 ph_collocated_ref_idx 两个参数来显示地指定使用哪一帧作为collocated picture。

ph_collocated_from_l0_flag 等于 1 指定用于TMVP collocated picture是从 RPL0 导出的。 ph_col located_from_l0_flag 等于 0 指定用于TMVP collocated picture是从 RPL1 导出的。当 ph_temporal_mvp_enabled_flag 和 pps_rpl_info_in_ph_flag 都等于 1 并且 num_ref_entries[1][RplsIdx[1]] 等于 0，则推断 ph_col located_from_l0_flag 的值等于 1。

ph_collocated_ref_idx 指定用于TMVP collocated picture的参考索引。当ph_collocated_from_l0_flag等于1时，ph_col located_ref_idx引用RPL0中的帧，并且ph_col located_ref_idx的值应在0到num_ref_entries[0][RplsIdx[0]]-1的范围内，包括0和num_ref_entries[0][RplsIdx[0]]-1。当ph_collocated_from_l0_flag等于0时，ph_col located_ref_idx引用RPL1中的帧，并且ph_col located_ref_idx的值应在0到num_ref_entries[1][RplsIdx[1]]-1的范围内，包括0和num_ref_entries[1][RplsIdx[1]]-1。

在VTM中，首先会在Lo和L1中寻找可以使用的参考帧，如果L0和L1的参考帧都可用，则选择其中QP比较大的帧，如果某个列表不可用，则选择另外一个列表，如果都不可用，则关闭TMVP。

Adaptive motion vector resolution (AMVR)

在 HEVC 中，当slice header中的 use_integer_mv_flag 等于 0 时，运动矢量差（MVD）（CU 的运动矢量和预测运动矢量之间）以四分之一亮度样本为单位用信号表示。在VVC中，引入了CU级自适应运动矢量分辨率（AMVR）方案。 AMVR允许CU的MVD以不同的精度进行编码。根据当前CU的模式（正常AMVP模式或仿射AVMP模式），可以如下自适应地选择当前CU的MVD：

– 正常 AMVP 模式：四分之一亮度样本、半亮度样本、整数亮度样本或四亮度样本。
– 仿射 AMVP 模式：四分之一亮度样本、整数亮度样本或 1/16 亮度样本。

如果当前CU具有至少一个非零MVD分量，则有条件地用信号发送CU级MVD分辨率指示。如果所有 MVD 分量（即，参考列表 L0 和参考列表 L1 的水平和垂直 MVD）均为零，则推断四分之一亮度样本 MVD 分辨率。

对于具有至少一个非零MVD分量的CU，用信号发送第一标志以指示是否将四分之一亮度样本MVD精度用于CU。如果第一标志为0，则不需要进一步的信令并且四分之一亮度样本MVD精度用于当前CU。否则，用信号发送第二标志以指示将半亮度样本或其他MVD精度（整数或四亮度样本）用于正常AMVP CU。在半亮度样本的情况下，半亮度样本位置使用 6 抽头插值滤波器而不是默认的 8 抽头插值滤波器。否则，用信号发送第三标志以指示对于正常AMVP CU使用整数亮度样本还是四亮度样本MVD精度。在仿射 AMVP CU 的情况下，第二个标志用于指示是使用整数亮度样本还是 1/16 亮度样本 MVD 精度。为了确保重建的 MV 具有预期的精度（四分之一亮度样本、半亮度样本、整数亮度样本或四亮度样本），CU 的运动矢量预测器将四舍五入为相同的精度。与 MVD 相加之前的精度与 MVD 的精度相同。运动矢量预测值向零舍入（即，负运动矢量预测值向正无穷大舍入，正运动矢量预测值向负无穷大舍入）。

编码器使用 RD 检查确定当前 CU 的运动矢量分辨率。为了避免总是对每个 MVD 分辨率执行四次 CU 级 RD 检查，在 VTM 中，仅有条件地调用除四分之一亮度样本之外的 MVD 精度的 RD 检查。对于普通 AVMP 模式，首先计算四分之一亮度样本 MVD 精度和整数亮度样本 MV 精度的 RD 成本。然后，将整数亮度样本MVD精度的RD成本与四分之一亮度样本MVD精度的RD成本进行比较，以决定是否有必要进一步检查四亮度样本MVD精度的RD成本。当四分之一亮度样本MVD精度的RD成本远小于整数亮度样本MVD精度的RD成本时，跳过四亮度样本MVD精度的RD检查。然后，如果整数亮度样本 MVD 精度的 RD 成本显着大于先前测试的 MVD 精度的最佳 RD 成本，则跳过半亮度样本 MVD 精度的检查。对于仿射 AMVP 模式，如果在检查仿射合并/跳过模式、合并/跳过模式、四分之一亮度样本 MVD 精度正常 AMVP 模式和四分之一亮度样本 MVD 精度仿射 AMVP 的速率失真成本后未选择仿射帧间模式，则不检查 1/16 亮度样本 MV 精度和 1-pel MV 精度仿射帧间模式。此外，在四分之一亮度样本MV精度仿射帧间模式中获得的仿射参数被用作1/16亮度样本和四分之一亮度样本MV精度仿射帧间模式中的起始搜索点。

HEVC Picture Buffering Management

1 POC and DPB

HEVC 中的每个图片都分配有一个图片顺序计数 (picture order count, POC) 值，表示为 PicOrderCntVal。它具有三个主要用途：唯一地标识图片，指示相对于同一 CVS 中其他图片的输出位置，以及在较低级别的 VCL 解码过程中执行运动矢量缩放。同一CVS中的所有图片必须具有唯一的POC值。来自不同CVS的图片可以共享相同的POC值，但是图片仍然可以被唯一地识别，因为不可能将来自一个CVS的图片与另一CVS的任何图片混合。 CVS 中允许 POC 值存在间隙，即，输出顺序连续的两个图片之间的 POC 值差异可以相差超过1（事实上，连续图片的 POC 值的差异量可以任意变化）。

图片的 POC 值由slice header 中的 slice_pic_order_cnt_lsb 码字表示。允许的 POC 值的范围是从 -2³¹ 到 2³¹ – 1，因此为了节省 slice header 中的比特，仅用信号通知 POC 值的最低有效位 (POC LSB)。用于 POC LSB 的位数可以在 4 到 16 之间，并在 SPS 中用信号通知。由于在 slice header 中仅用信号通知 POC LSB，因此当前图片的最高有效 POC 值位 (POC MSB) 是从称为 prevTid0Pic 的先前图片导出的。为了即使图片被移除，POC 推导也能以相同的方式工作，prevTid0Pic 被设置为时间层 0 的最近的先前图片，该图片不是 RASL 图片、RADL 图片或子层非参考图片。解码器通过将当前图片的POC值与前一个图片的POC值进行比较来导出POC MSB值。

HEVC中的解码图片缓冲器(DPB)是包含解码图片的缓冲器。除当前图片之外的解码图片可以存储在DPB中，因为它们需要参考，或者因为它们尚未输出，这是启用乱序输出所必需的。请注意，当前解码的图片也存储在 DPB 中。图 2.12 显示了两个示例引用结构，它们都需要至少三张图片的 DPB 大小。图2.12a中的图片P1和P2都在P3之后输出，因此在P3解码时都需要将其存储在DPB中。因此，DPB 需要能够同时存储 P1、P2 和 P3。在图2.12b中，每个图片使用两个参考图片，因此DPB也需要足够大以同时存储三个图片。图2.12b中的参考结构是所谓的低延迟B结构的示例，其中广泛使用双向预测而没有任何乱序输出。

解码器需要分配用于解码特定比特流的最小DPB大小由sps_max_dec_pic_buffering_minus1 码字来发信号通知，其可以针对序列参数集中的每个时间子层发送。 HEVC的第一版本中允许的最大可能的DPB大小是16，但是根据图片大小和所使用的解码能力的“级别”的组合，最大大小可以进一步受到限制。请注意，HEVC 指定要包括在 DPB 中的当前图片，因此 DPB 大小为 1 将不允许任何参考图片。如果DPB大小为1，则所有图片都必须进行帧内编码。

DPB中的图片被标记以指示它们的参考状态。 DPB中的每张图片都被标记为“不用于参考”、“用于短期参考”或“用于长期参考”。通常将这些类型的图片分别称为非参考图片、短期图片和长期图片。

参考图片要么是短期图片，要么是长期图片。不同之处在于，长期图片可以在DPB中保存的时间比短期图片长得多。有一条规则决定了短期图片可以在DPB中停留多长时间。由当前图片、prevTid0Pic、DPB中的短期参考图片和DPB内等待输出的图片组成的图片集的POC跨度必须在POC LSB覆盖的POC范围的一半以内。该规则保证了POC MSB推导的正确性，并通过使解码器能够识别丢失的短期图片来提高误差鲁棒性。

非参考图片是不用作参考但如果以后需要输出时仍可以保留在DPB中的图片。

如图 2.13 所示，每个解码图像的图像标记都会发生变化。图片被解码后，最初总是被标记为短期图片。短期图片可以保持短期图片或改变为非参考图片或长期图片。长期图片可能会保持长期图片或变成非参考图片，但它们永远不能再变成短期图片。非参考图片永远不能再次成为参考图片。

DPB中的图片可以被保存以供将来输出，无论它是参考图片还是非参考图片。当图片已被解码时，它通常等待输出，除非 slice header 中的pic_output_flag等于0或者图片是与CVS中的第一图片相关联的RASL图片。如果是这种情况，则不会输出图片。

图片标记和图片输出是在单独的过程中完成的，但是当图片既是非参考图片并且不等待输出时，DPB中的图片存储缓冲器被清空并且可以用于存储将来的解码图片。编码器负责管理图片标记和图片输出，以便 DPB 中的图片数量不超过 sps_max_dec_pic_buffering_minus1 指示的 DPB 大小。

SPS中与图片输出相关的另外两个码字是
sps_max_num_reorder_pics 和 sps_max_latency_increase_plus1，两者都可以针对每个时间子层发送。 sps_max_num_reorder_pics，此处表示为NumReorderPics，指示在解码顺序中可以在任何图片之前并且在输出顺序中在其之后的图片的最大数量。图 2.12a 中的参考结构的 NumReorderPics 值为 2，因为图片 P3 有两个图片在解码顺序上位于其前面，但在输出顺序上位于其后面。图 2.12b 的 NumReorderPics 为零，因为没有图片乱序发送。

sps_max_latency_increase_plus1 用于指示 MaxLatencyPictures，它指示在输出顺序中可以在任何图片之前并且在解码顺序中在该图片之后的图片的最大数量。图 2.14 显示了 NumReorderPics 和 MaxLatencyPictures 之间的区别。 NumReorderPics 在此等于 1，因为 P1 是唯一乱序发送的图片。 MaxLatencyPictures 设置为 4，因为图片 P2、P3、P4 和 P5 在输出顺序上都先于 P1。此参考结构的最小 DPB 大小为 3。

可以说NumReorderPics表示DPB中处理乱序图片所需的图片存储的最小数量，而MaxLatencyPictures表示由乱序图片引起的以图片为单位的最小编码延迟量。

对于低延迟应用，建议使用不会因乱序输出而导致编码延迟的参考结构。这是通过确保解码顺序和输出顺序相同来实现的，这可以通过发信号通知 NumReorderPics 或 MaxLatencyPictures 或两者都等于 0 来表示。

2 Reference Picture Sets

将图片标记为“用于短期参考”、“用于长期参考”或“不用于参考”的过程是使用参考图片集（RPS）概念来完成的。 RPS是在每个slice header中用信号通知的一组图片指示符，并且由一组短期图片和一组长期图片组成。在图片的第一个片头被解码之后，DPB中的图片被标记为由RPS指定的。

RPS的短期图片部分中指示的DPB中的图片被保留为短期图片。将RPS中的长期图像部分中指示的DPB中的短期或长期图像转换为或保留为长期图像。最后，DPB中RPS中没有指示符的图片被标记为未使用以供参考。因此，可以用作对按照解码顺序的任何后续图片进行预测的参考的所有已经解码的图片必须被包括在RPS中。

RPS 由一组图片顺序计数 (POC) 值组成，用于识别 DPB 中的图片。除了用信号发送 POC 信息之外，RPS 还为每张图片发送一个标志。每个标志指示对应的图片是否可供当前图片参考。注意，即使参考图片被信号通知为对于当前图片不可用，它仍然被保存在DPB中并且可以供稍后参考并用于解码未来的图片。根据 POC 信息和可用性标志，可以创建如表 2.3 所示的五个参考图片列表。

列表RefPicSetStCurrBefore由可用于当前图片的参考并且具有低于当前图片的POC值的POC值的短期图片组成。 RefPicSetStCurrAfter 由可用的短期图片组成，其 POC 值高于当前图片的 POC 值。 RefPicSetStFoll是包含对于当前图片不可用但可以用作用于按解码顺序解码后续图片的参考图片的所有短期图片的列表。最后，列表RefPicSetLtCurr和RefPicSetLtFoll分别包含可用于和不可用于当前图片的参考的长期图片。

图 2.15 和表 2.4 显示了使用三个时间子层的示例引用结构以及按解码顺序排列的每个图片的 RPS 列表的内容。

IDR图片重置编解码器，包括将DPB中的所有图片转变为非参考图片。由于IDR图片的RPS是空的，因此没有为IDR图片用信号发送RPS语法。因此表 2.4 中的所有列表对于 IDR 图片 I0 都是空的。在图片B3处，图片P1被放入RefPicSetStFoll中，因为P1未被B3引用。然而，P1 保留在 DPB 中，因为它用于将来的图片。在图片B4处，本例中I0被制作为长期图片，因此由于B4没有引用它，因此将其放入RefPicSetLtFoll中。在图片P5处，编码器通过根本不将图片B2和B3包括在RPS中来使图片B2和B3成为非参考图片。同时，图片 I0 被移动到 RefPicSetLtCurr，因为它被 P5 引用。此后，I0 保存在 RefPicSetLtFoll 中以供以后使用。

编码器需要确保RefPicSetStCurr和RefPicSettRoll中指示的每个图片都存在于DPB中。如果不是这种情况，解码器应该将其推断为比特流错误，并采取适当的行动。然而，如果在RPS中的条目的DPB中不存在被指示不用于当前图片的参考的对应图片，则解码器不采取任何动作，因为这种情况可能由于移除个别子层非参考图片或整个较高时间子层而发生。

尽管没有针对IDR图片发送RPS，但是CRA和BLA图片都可以在其RPS中具有图片，使得相关联的RASL图片可以使用RPS中的那些图片作为预测的参考。但是，对于CRA和BLA图片，要求RefPicSettCurr和RefPicSetLtCurr列表均为空。

3 Reference Picture Set Signaling

对于RPS中的每个图片，用信号发送三条信息：POC信息、可用性状态以及图片是短期图片还是长期图片。

短期图片的 POC 信息以两组方式发送。组 S0 首先被发信号通知，它由 POC 值低于当前图片的所有短期图片组成。该组之后是组 S1，其包含具有比当前图片更高的 POC 值的所有短期图片。每组的信息按照相对于当前图片的POC距离顺序发送，从最接近当前图片的POC值的POC值开始。对于每张图片，都会发出相对于前一张图片的 POC 增量信号。当前图片充当每组中第一张图片的前一张图片，因为第一张图片没有前一张图片。

通过 POC 增量对长期图片进行编码可能会导致非常长的码字，因为长期图片可以在 DPB 中保留很长时间。因此，长期图像而是通过其 POC LSB 值来表示。用于slice header POC LSB 值的相同位数也用于长期图片。解码器会将 RPS 中发信号通知的每个 POC LSB 值与 DPB 中图片的 POC LSB 值进行匹配。由于 DPB 中可能有多个具有相同 POC LSB 值的图片，因此还可以选择发送长期图片的 POC MSB 信息。当存在解码器无法正确识别图片的风险时，必须发送此 MSB 信息。避免这种风险的一种方法是，当相应的 POC LSB 值已被两个或多个不同的长期图片使用时，始终用信号发送长期图片的 POC MSB 信息。

RPS 中每个图片的可用性状态由一位标志表示，其中“1”表示该图片可供当前图片参考，“0”表示不可用。

表 2.5 显示了图 2.15 中图片 B7 的示例 RPS 语法。表中的第一列显示语法是否与发信号通知短期图片或长期图片相关。第二列包含每个语法元素的 HEVC 规范名称。第三列表示RPS中的相关图片，第四列表示示例中语法元素的值。第五列显示语法元素的类型，其中“uvlc”表示通用可变长度代码，“flag”是一位二进制标志，“flc”是固定长度代码。最后一列显示使用类型对每个语法元素的值进行编码的结果位。

图2.15中图片B7的POC值为5，其RPS包含3个短期图片； S0组中的图片P1和S1组中的图片B6和P5。 RPS 的前两个语法元素传达 S0 和 S1 中的图片数量；这是由 uvlc 代码“010”和“011”编码的。然后用信号发送组S0中的图像。 P1 的 POC 增量为 1，因为它的 POC 值为 4，并且当前图片的 POC 值等于 5。在编码之前，POC 增量减去 1，因此最终信号值为 0，这导致 uvlc 代码“1” 。当前图片B7以图片P1为参考；这是由标志“1”表示的。

接下来的语法元素涵盖了 S1 中的图片。当前图片的 POC 值等于 5，因此代码字“1”用于 B6，因为其 POC 值等于 6。图片 B6 也用于由标志“1”指示的当前图片的参考。 S1 中的第二张图片是 P5，其 POC 值为 8。它是相对于 S1 中的前一张图片（B6，POC 值为 6）进行编码的。增量为 2，减 1 等于 1，编码为 ‘010’。当前图片B7不参考图片P5；这是由标志“0”表示的。

RPS 中的下一个码字表示 RPS 中长期图像的数量，它是 1，并且使用“010”进行 uvlc 编码。然后用信号通知长期图像I0的POC LSB值。这是通过代码字“00000000”假设 8 位用于发送 POC LSB 值。长期图片I0不被当前图片B7参考；这是用标志‘0’来表示的。最后，由于 DPB 中没有其他图片共享相同的 POC LSB 值，因此不会针对该长期图片发送 POC MSB 信息；这是用当前标志“0”来表示的。

出于弹性原因，RPS信息在每个 slice header 中用信号发送，但是对于每个 slice 按原样重复RPS信息可能会花费许多比特。不仅可以将图片分割成必须重复RPS的多个slice，比特流中的图片通常通过重复相同的GOP结构来编码，因此对于在GOP结构中共享相同位置的图片重复相同的RPS信息。

为了利用冗余并降低总体比特成本，可以在 SPS 中发送一些 RPS 语法在 slice header 中引用。 RPS的短期图像部分是相对于当前图像的POC值进行编码的。这使得可以将多个短期RPS部分存储在SPS中的列表中，并且仅在 slice header 中用信号发送列表索引。该列表可以包含用于GOP结构中的每个画面位置的一个RPS。然后，SPS 中的 RPS 数量将等于 GOP 长度，并且每个片将仅需要发送列表索引以便用信号通知其短期图像部分。

发送每个GOP位置的RPS信息可能需要SPS中相对较多的比特，比如对于一些GOP结构存在数百比特。为了节省 SPS 中的比特，HEVC 中可以选择使用 RPS 预测。这要求以 GOP 解码顺序发送 RPS，并利用每个 RPS 与前一个类似的事实。可以按照解码顺序将图片参考从一个RPS移除到下一个RPS，但是相对于前一RPS最多只能添加一张新图片。 HEVC 中的 RPS 预测机制正在利用此属性，相对于显式信令，可以实现 SPS 中 RPS 比特数最多减少 50%。

4 Reference Picture Lists

当P或B slice的 slice header 已被解码时，解码器为当前slice设置参考图片列表。有两个参考图片列表，L0和L1。 L0 用于 P 和 B slice，而 L1 仅用于 B slice。图2.16示出了使用五个参考图片进行预测的图片B7的参考图片列表示例。

首先，构建 L0 和 L1 的临时列表。临时列表L0以RPS列表RefPicSetStCurrBefore中的图片开始，按POC值降序排序。这些都是可供当前图片参考并且具有小于当前图片的POC值的POC值的短期图片。因此图2.16中图片B7的临时列表L0以P1开始，随后是B2。接下来是按 POC 值升序排序的 RPS 列表 RefPicSetStCurrAfter 中的图片，即图 2.16 中的 B6 和 P5。最后添加可用的长期图片，因此图片I0是最后添加的图片。图片B7的最终临时列表L0则为{P1、B2、B6、P5、I0}。临时列表L1的设置与L0类似，但是RefPicSetStCurrBefore和RefPicSetStCurrAfter的顺序交换。因此，图片B7的临时列表L1变为{B6、P5、P1、B2、I0}。

临时列表用于构建最终的L0和L1列表。L0和L1的长度在PPS中用信号发送，但可以被slice header 中的可选码字覆盖。列表的最大长度为15。如果L0或L1的指定长度分别小于临时列表L0或L2的长度，则通过截断相应的临时列表来构建最终列表。如果指定的长度大于相应临时列表的长度，则从临时列表中重复图片。例如，如果长度为2，L0等于{P1、B2}，如果长度是9，则等于{P1，B2、B6、P5、I0、P1、B2、B6、P5}。启用比临时列表长的列表的原因是加权预测，以使不同的加权因子能够应用于相同的参考图片。

从临时列表构建 L0 和 L1 的另一种方法是通过显式列表信令。在这种情况下，列表中的每个条目都有一个代码字，用于指定要使用临时列表中的哪个图片。因此，如果指定L0的长度等于3，则有3个码字用于指定L0。例如，如果这三个码字等于1、1、0，则当P1是临时列表L0中的第一图片且B2是第二图片时，列表L0变为{B2、B2、P1}。

最终列表L0和L1用于运动补偿。对于单预测，为块指示一个运动向量和一个参考图片索引。例如，如果块的信号索引等于 0，则 L0 中的第一张图片是用于运动补偿的图片。

ISP (Intra Subpartition Mode)

内部子分区（ISP）模式是VVC中新引入的工具之一。它是一种分区机制，旨在对帧内预测块的非平稳特征进行建模。具体来说，ISP将一个块的亮度分量垂直或水平地分割成K个大小相等的子分区，这些子分区以顺序的方式一一处理。

Layout

帧内子分区 (ISP) 根据块大小将亮度帧内预测块垂直或水平划分为 2 或 4 个子分区。例如，ISP 的最小块大小为 4×8（或 8×4）。如果块大小大于 4×8（或 8×4），则相应的块将被划分为 4 个子分区。值得注意的是，M × 128（M ≤ 64）和 128 × N（N ≤ 64）ISP 块可能会对 64 × 64 VDPU 产生潜在问题。例如，single-tree 情况下的M×128 CU具有M×128亮度TB和两个相应的M/2×64色度TB。如果CU使用ISP，则亮度TB将被分为4个M×32TB（只能水平分割），每个TB小于64×64块。然而，在当前的ISP设计中，色度块没有被划分。因此，两个色度分量的大小都将大于 32 × 32 块。类似地，使用 ISP 的 128 × N CU 也可以有类似的情况。因此，这两种情况对于 64 × 64 解码器管道来说是一个问题。因此，可以使用 ISP 的 CU 大小限制为最大 64 × 64。图 19 显示了两种可能性的示例。所有子分区都满足至少有16个样本的条件。

Processing

如果是水平分割，则从上到下逐一处理子分区；如果是垂直分割，则从左到右处理。每个子分区的编码方式与任何其他帧内预测块相同：首先，使用子分区的相邻样本生成预测，并获得相应的残差信号。后者被变换和量化，变换系数被熵编码并发送到解码器。最后，得到的重建样本可以用来生成下一个子分区的预测。此过程一直持续到所有子分区都已编码为止。

然而，对于宽度小于4的子分区，在上述过程中有一个例外。这是因为典型的硬件架构使用光栅扫描模式分配样本，然后以4×1组的方式访问它们。对于这样的设计，1×H和2×H的子分区可能构成一个问题。因此，ISP的最小预测宽度为4个样本，如下所示：不是在TB级别执行每个预测，而是将TB分组在4×H区域中，这些区域仅使用相邻样本作为参考进行一次预测。这保证了可以同时处理每个4×H区域内的TB。例如，一次预测一个垂直分割的4×16 CU，然后并行处理相应的四个1×16 TB。

Prediction

在使用ISP的CU内，所有子部分都应用相同的帧内预测模式，因此只需要对其进行一次编码。ISP帧内预测模式可以从任何传统的帧内预测方式中选择，即Planar、DC和角度方式，其中对于后一种方式，根据CU宽高比执行角度方式向广角方式的转换。PDPC以与非ISP情况相同的方式应用于所有ISP子分区，前提是它们的宽度和高度至少为4。此外，参考样本滤波过程和帧内插值滤波器选择的条件不再存在，并且在ISP模式下，DCT-IF 滤波器总是用于分数位置插值。如果一个块的MRL索引不是0，则ISP编码模式将被推断为0，因此ISP模式信息将不会发送到解码器。

Transforms

为了降低信令成本，ISP总是使用隐式多变换选择(MTS)。因此，编码器不会对每个结果子分区的不同可用变换执行RD测试。ISP模式的变换选择将改为固定的，并根据所使用的帧内模式、处理顺序和块大小进行选择。因此，不需要任何信号。例如，设t_h和t_v是分别为w×h子分区，其中w是宽度h是高度。然后根据以下规则选择变换：

如果w＝1或h＝1，则分别不存在水平变换或垂直变换。
如果w≥4且h≤16，则t_h=DST-VII，否则，t_h=DCT-II
如果h≥4且h≤16，则t_w=DST-VII，否则，t_w=DCT-II

其次，低频不可分离变换(LFNST)是针对整个ISP块全局用信号发送的，因此，相同的LFNST矩阵用于具有非零编码块标志(CBF)的所有子分区。只有当所有子分区都满足zero-out条件时，LFNST才能用于ISP-CU。非ISP情况下的LFNST转换内核也用于ISP。因此，如果子分区的宽度或高度小于4，则不能将LFNST用于ISP。

Coefficient coding and signalization

子分区的残差信号的系数以与 VVC 中的常规块相同的方式进行熵编码，并进行以下修改：

每个子分区的编码块标志（CBF）的上下文是先前编码的子分区的CBF的值（在第一个子分区的情况下，默认值为0）。
使用ISP的块的至少一个CBF被假定为非零。因此，如果一个块包含 n 个子分区，并且前 n-1 个子分区的 CBF 为零，则第 n 个 CBF 被推断为1，因此不会显式地用信号通知它。
如果子分区是一行，则最后位置语法元素仅需要发送一个坐标。
令 w 和 h 分别为每个子分区的宽度和高度。然后，如果 w ≥ 8 且 h ≤ 2，系数子块将具有 16/h × h 的形状。类似地，如果 w ≤ 2 并且 h ≥ 8，系数子块将具有 w × 16/w 形状。在所有其他情况下，它们将具有与常规帧内预测块中使用的相同的 4 × 4 形状。结果，所有系数子块将具有 16 个样本。

关于信令，为每个块添加了两个新的语法元素：第一个是指示当前块是否使用 ISP 的标志（仅适用于不使用 MRL 的非 4×4 亮度块）。当使用 ISP 时，会发送第二个标志，指定使用哪种类型的分割（水平或垂直）。此外，这两个新标志使用一个上下文自适应二进制算术编码（CABAC）。请注意，如果只能进行一次分割（例如，128 × 64 块只能垂直分割），则在解码器侧推断出该标志，因此不会传输该标志。

二值化过程(Binarization process)

VVC标准中使用了4种二值化方案：截断莱斯码(truncated Rice (TR)), 截断二进制码(truncated binary (TB)), k阶指数哥伦布码(k-th order Exp-Golomb (EGk)), 定长码(fixed-length (FL))。

TR码

TR码由前缀和后缀组成，后缀可能不存在。TR码有3个输入，分别是：语法元素值 symbolVal、门限值 cMax 和莱斯参数 cRiceParam。语法元素值 symbolVal 的前缀值 prefixVal 定义如下：

prefixVal = symbolVal >> cRiceParam

如果 prefixVal 小于 cMax >> cRiceParam，则前缀码由 prefixVal 个1和0组成。下表给出了这种一元二值化的码表：

如果 prefixVal 大于等于 cMax >> cRiceParam，则前缀码由 cMax >> cRiceParam 个1组成。

当 cMax 大于 symbolVal 且 cRiceParam 大于0时，TR码的后缀存在，后缀值推导如下：

suffixVal = symbolVal − ( prefixVal << cRiceParam )

TR 码的后缀通过定长码(FL)为 suffixVal 进行二值化，cMax 值等于 ( 1 << cRiceParam ) − 1。

TB码

TB码的输入有两个，分别为语法元素值 synVal 和门限值 cMax。TB码的推导过程如下：

n = cMax + 1
k = Floor( Log2( n ) )
u = ( 1 << ( k + 1 ) ) − n

如果 synVal 小于 u，则通过定长码(FL)为 synVal 进行二值化，其中 cMax 值等于 ( 1 << k ) − 1。否则，通过定长码(FL)为 (synVal+u) 进行二值化来导出TB码，其中 cMax 值等于(1<<(k+1))−1。

k阶指数哥伦布码

k阶指数哥伦布码包括前缀码和后缀码，输入为语法元素值 symbolVal 和阶数 k，输出的二进制串定义如下，其中函数put(X)是将X放在二进制串的末尾。

absV = Abs( symbolVal )
stopLoop = 0
do
if( absV >= ( 1 << k ) ) {
put( 0 )
absV = absV − ( 1 << k )
k++
} else {
put( 1 )
while( k−− )
put( ( absV >> k ) & 1 )
stopLoop = 1
}
while( !stopLoop )

下表给出了0阶指数哥伦布码的前缀码和后缀码

下表给出了无符号0阶指数哥伦布码，对应语法元素表中的ue(v)

对于有符号的0阶指数哥伦布码，对应语法元素表中的se(v)，VVC标准中采用了映射的方法，映射表为：

FL码

FL 码是通过使用符号值 symbolVal 的固定长度位无符号整数二进制串来构造的，其中fixedLength = Ceil( Log2( cMax + 1 ) )。 FL 码的 bin 索引使得 binIdx = 0 与最高有效位相关，并且 binIdx 的值向最低有效位递增。

Geometric Partitioning Mode in Versatile VideoCoding

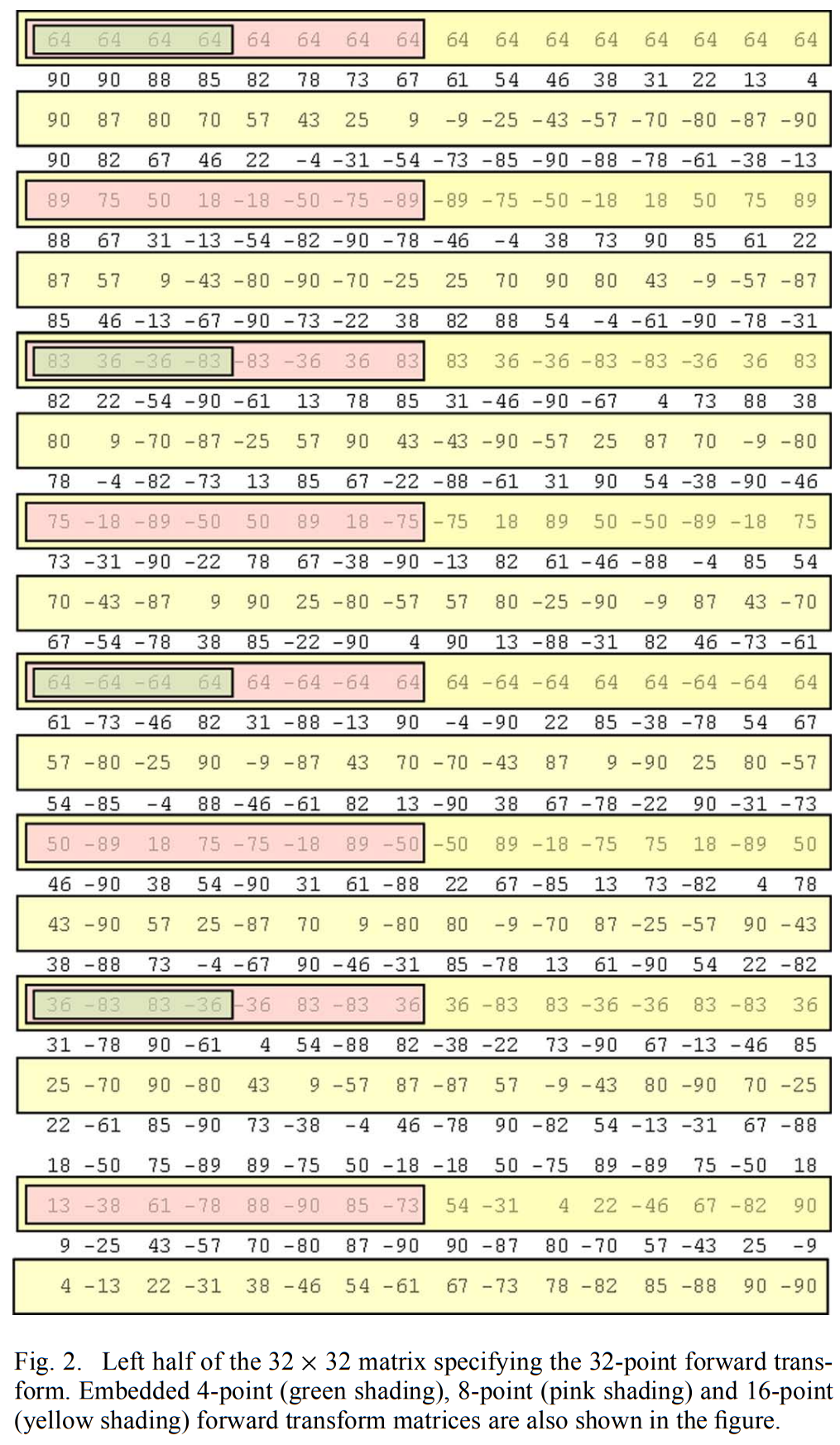
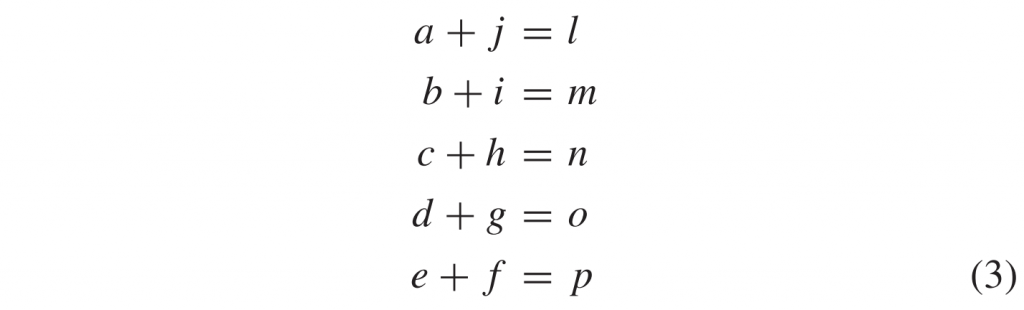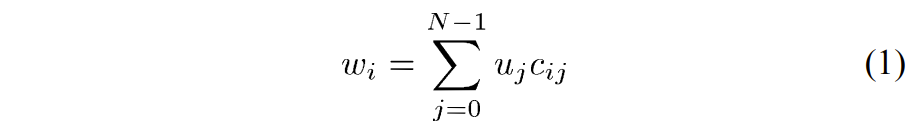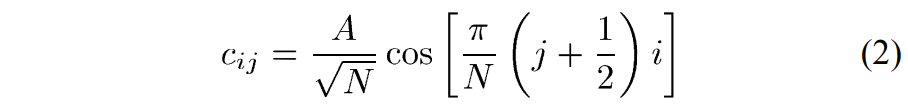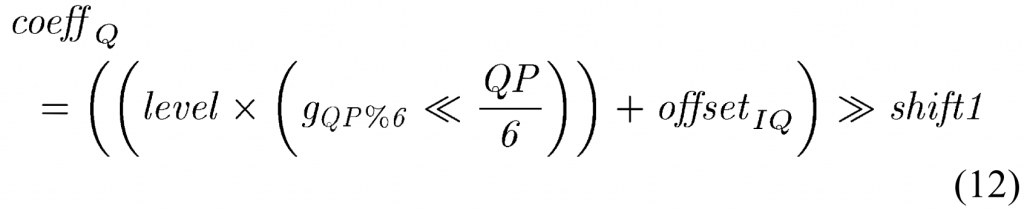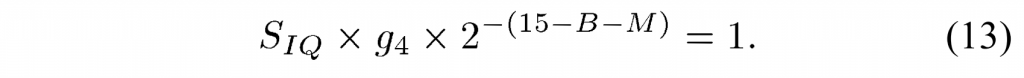H. Gao, S. Esenlik, E. Alshina, and E. Steinbach, “Geometric partitioning mode in versatile video coding: Algorithm review and analysis,” IEEE Trans. Circuits Syst. Video Technol., early access, Nov. 24, 2020

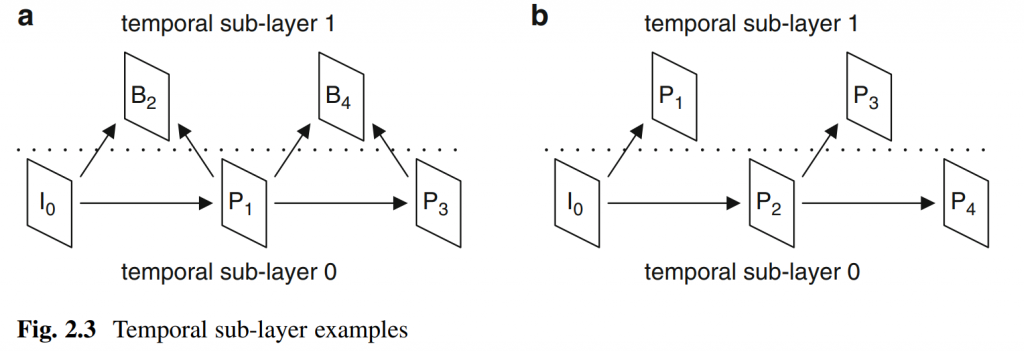
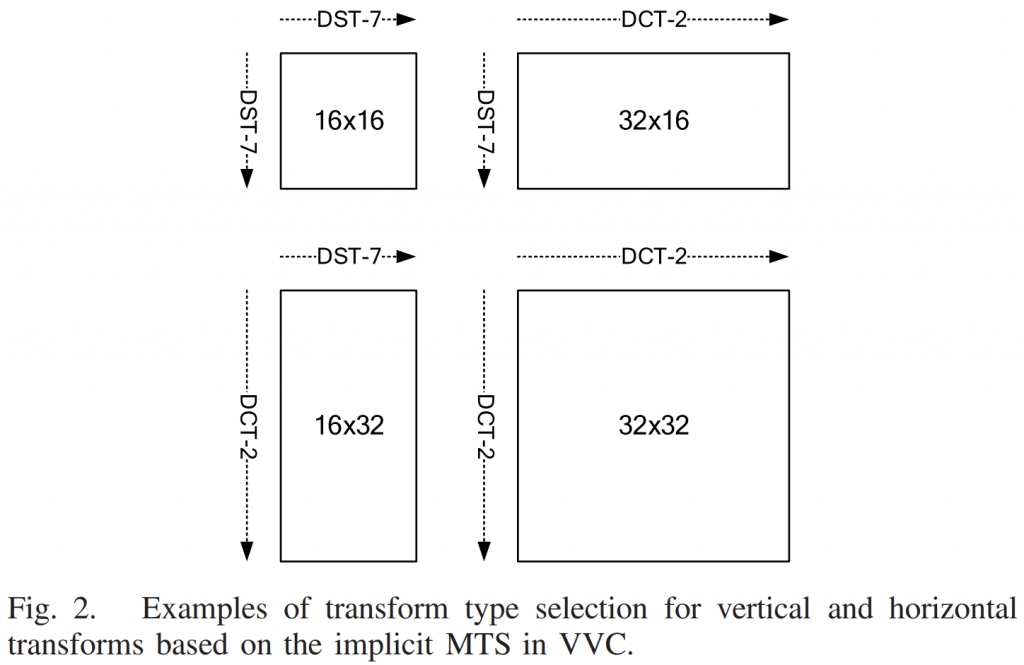
对于自然视频内容，矩形块划分对于 MCP (motion compensated prediction)来说不是最佳选择。视频序列中图片的运动场通常由运动物体的边界来分割，如图2(a)和图2(b)所示。这是因为对象通常表现出相对于静态背景或其他移动对象的移动，并且自然序列中的对象边界很少遵循矩形块图案。如图2(c)所示，当使用矩形块来近似移动对象边界时，需要更精细的块划分，这增加了用于用信号通知这些块的划分和预测语法元素的速率开销。此外，近似的分割边界很少遵循实际的运动场边界。因此，预测误差更高，这增加了残差信令的比特率。

为了提高划分精度，基于分割的划分方法被集成到现有的视频编码标准结构中。在基于分割的划分方法中，划分图是通过在编码器处对参考图片中的参考块应用分割算法来获得的。在解码器处应用相同的分割算法以避免分割图的变换。当前块被划分图分成多个分区，每个分区或者单独地与其关联的MV执行MCP或者从其他分区导出样本值。可以向解码器发送额外的MV或者在解码器侧导出额外的MV以指示应用分割算法的参考块的位置。尽管基于分割的分割方法很好地近似了对象的实际轮廓，但像素精确的分割算法显着增加了计算复杂性并导致硬件实现困难，特别是在解码器处。此外，基于分割的分割方法无法有效地处理大块或包含由复杂纹理引起的多个边缘的块，例如图2(b)的左侧。

在 HEVC 和 VVC 的开发过程中，几何划分方案及其变体已在文献中提出并在核心实验 (CE) 中进行了研究。几何划分方案旨在提高划分精度并最小化解码器端的计算复杂度和实现难度。代替分割算法，使用一组预定义的直线将矩形块几何分割成两个分区，如图2(d)中的示例所示。每个分区与其运动信息相关联并单独执行MCP。运动信息和划分信息被发送到解码器。该块由解码器侧解析的运动和划分信息直接重建。因此，几何划分方案的解码器复杂度增加较小。

A. Core Algorithm of GPM in VVC

由于VVC中的帧内预测CU可以使用角度和非线性预测模式，非水平和非垂直边缘得到了很好的处理。因此， GPM 重点关注帧间预测的 CU。当GPM应用于CU时，该CU被直线划分边界分成两部分。划分边界的位置在数学上由角度参数 \(\varphi\)和偏移参数 \(\rho\) 定义。这些参数被量化并组合成GPM划分索引查找表。当前CU的GPM划分索引被编码到比特流中。总的来说，VVC 中的 GPM 支持 64 种划分模式，对于尺寸为 \(w\times h={2^k}\times2^l\)的亮度 CU，其中 \(k,l~\in~{3\ldots6}\)。此外，GPM 在宽高比大于 4:1 或小于 1:4 的 CU 上被禁用，因为窄 CU 很少包含几何划分的图案。

两个 GPM 分区包含用于预测当前 CU 中相应部分的单独运动信息。 GPM 的每个部分只允许使用单向 MCP，因此 GPM 中 MCP 所需的内存大小等于常规双向 MCP 的大小带宽。为了简化运动信息编码并减少GPM可能的组合，运动信息采用Merge模式进行编码。 GPM Merge候选列表源自传统的Merge候选列表，以确保仅包含单向运动信息。

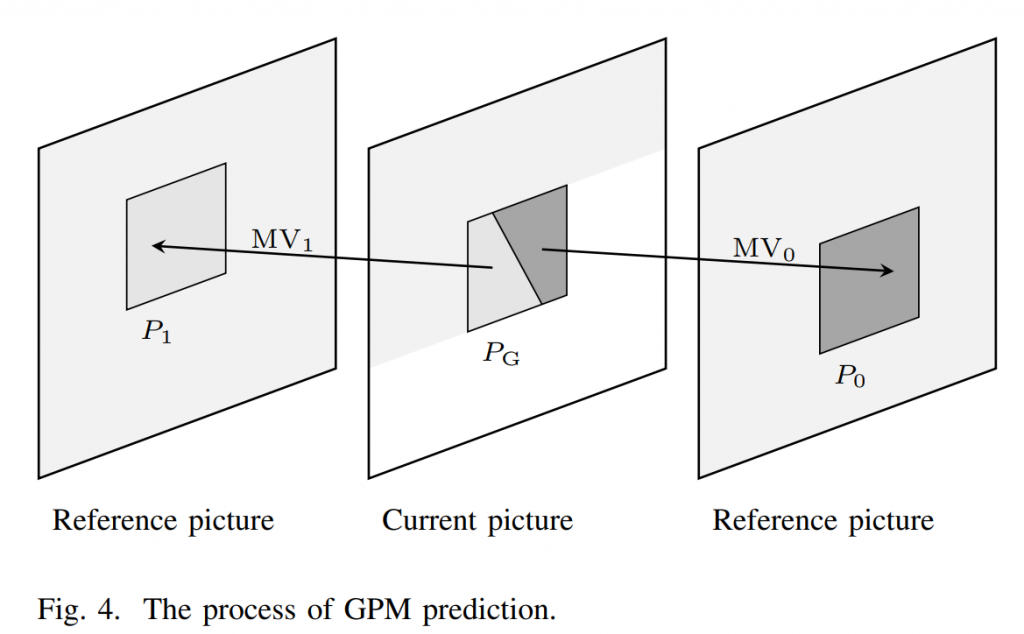
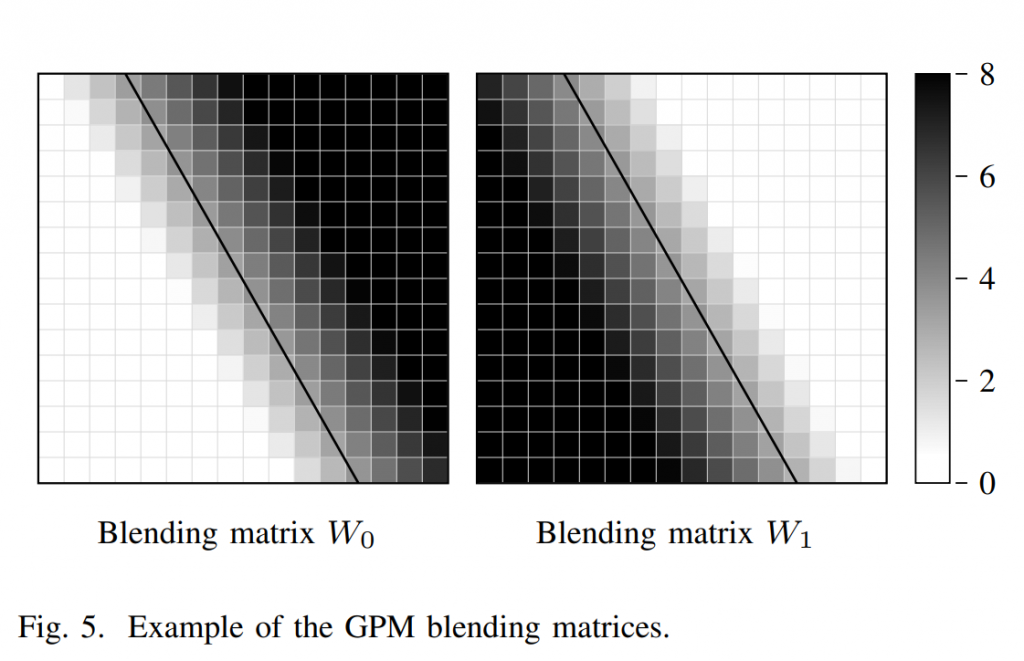
图4说明了GPM的预测过程。当前CU的右侧预测部分（大小为w×h）由MV0从P0预测，而左侧部分由MV1从P1预测。最终的 GPM 预测 PG 是通过使用整数混合矩阵 W0 和 W1 执行混合过程生成的，包含的权重范围为 0 到 8。这可以表示为(1)：

\(P_{\mathrm{G}}=(W_0\circ P_0+W_1\circ P_1+4)\gg3\)

其中(2)：

\(W_0+W_1=8J_{w,h},\)

其中 J_w,h 是大小为 w × h 的矩阵。混合矩阵的权重取决于样本位置和分区边界之间的位移。图 5 显示了一组示例混合矩阵。混合矩阵推导的计算复杂度极低，因此这些矩阵可以在解码器侧即时生成。

然后从原始信号中减去GPM预测的P_G以生成残差。使用常规 VVC 变换、量化和熵编码引擎将残差变换、量化并编码到比特流中。在解码器侧，通过将残差添加到 GPM 预测 P_G 来重建信号。当残差可以忽略不计时，GPM 还支持Skip模式。

B. Partitioning Boundary Definition and Quantization

1）划分边界的定义：划分边界定义为几何上位于CU内部的直线。这条直线的方程用 Hessian 范式表示为(3)：

\(x_\mathrm{c}~\cos(\varphi)-y_\mathrm{c}~\sin(\varphi)+\rho=0\)

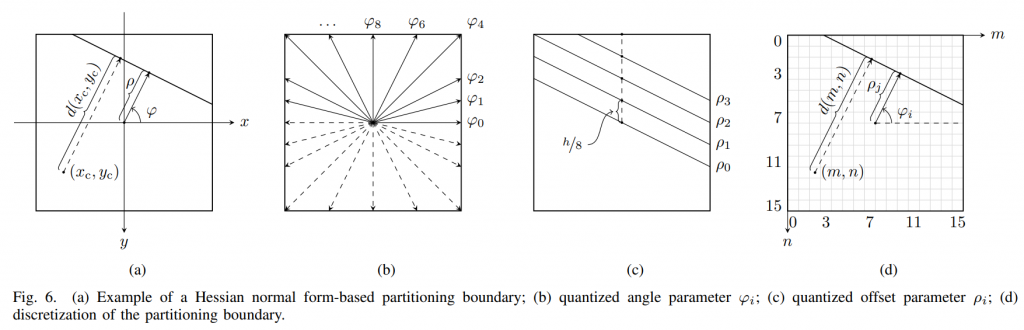
其中(x_c，y_c)定义与CU的中心位置相关的连续位置。在图6(a)所示的示例中，(3)中的角度参数\(\varphi\)描述了从x轴到分割边界法向量的逆时针角度，而(3)中的偏移参数 \(\rho\) 是划分边界从CU中心定义的原点的位移。请注意，y轴被反转以简化分区边界的离散化。

任意位置(x_c，y_c)相对于分割边界的位移d用于导出混合矩阵W₀和W₁。根据(3)，d的值给出为(4)：

\(d(x_\mathrm{c},y_\mathrm{c})=x_\mathrm{c}\mathrm{~}\cos(\varphi)-y_\mathrm{c}\mathrm{~}\sin(\varphi)+\rho.\)

由于位移是有方向的，因此 d 的值可以是正值或负值。 d 的符号表示位置 (x_c, y_c) 属于哪个分区，而 d 的大小等于 (x_c, y_c) 到分区边界的距离。

2）角度参数\(\varphi\)的量化：为了实现合理数量的定义的划分边界，必须对角度参数\(\varphi\)和偏移参数\(\rho\) 进行量化。如图 6（b）所示，角度参数\(\varphi\)被量化为 20 个离散角度 \(\varphi_i\)，范围 [0, 2π) 对称划分。由于对角线或反对角线分割边界在 GPM 中最常用，因此量化的\(\varphi_i\)被设计为固定\(\tan(\varphi_i)\) 值，该值等于应用 GPM 的 CU 的可能长宽比。例如，如果将 GPM 应用于宽高比 w/h = 1/2 的 CU，则对角线分区边界与由 \(\varphi_i~=~\arctan(1/2)\) 和 \(\rho=0\) 定义的 (3) 线对齐。在所提出的 GPM 算法中，\(\tan(\varphi_i)\) 被限制为 {0, ±1/4, ±1/2, ±1, ±2, ∞} 中的值。请注意，不包括产生接近水平划分边界的±4的正切值，因为运动场的接近水平划分不太频繁地用于自然视频内容。

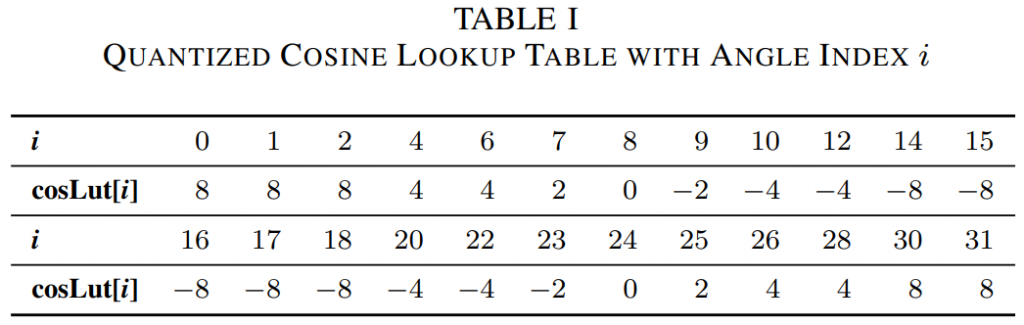
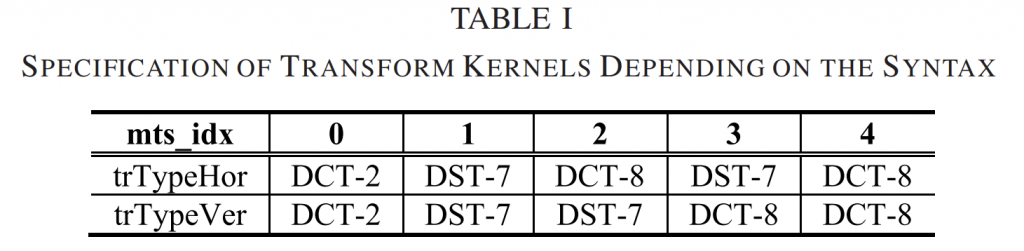
根据基于正切值的角度参数量化，(4) 中的 \(\cos(\varphi_i)\) 被离散化为表 1 所示的 3 位精度查找表。 cosLut[·] 的输入 i 是量化 \(\varphi_i\)的角度索引。请注意，表 I 中的一些未使用的角度索引 i 值被跳过。基于三角恒等式，\(sin\varphi_i\)的离散化查找表可以很容易地导出(5)：

\(\operatorname{sinLut}[i]=-\operatorname{cosLut}[(i+8)\%32]\)

因此，(4)被重写为(6)：

\(d(x_c,y_c)=(x_c\cdot cosLut[i])\gg3+(y_c\cdot cosLut[(i+8)\%32])\gg3+\rho\)

3）偏移参数\(\rho\)的量化：图6(c)示出了偏移参数\(\rho\)量化的示例。根据CU宽度w和高度h，偏移参数\(\rho\)被量化为\(\rho_j\)。偏移索引 j = {0 … 3}。为了避免不同块大小之间分布不均匀的分区边界偏移，首先将 \(\rho_j\)分解为(7)：

\(\rho_j=\rho_{x,j}\cos(\varphi_i)-\rho_{y,j}\sin(\varphi_i)\)

或(8):

\(\begin{aligned}\rho_j&=(\rho_{x,j}\cdot\cos\text{Lut}[i])\gg3\\&+(\rho_{y,j}\cdot\cos\text{Lut}[(i+8)\%32])\gg3.\end{aligned}\)

然后使用 ρ_x,j 和 ρ_y,j与 w 和 h 耦合(9)：

\(\rho_{x,j}=\begin{cases}0&i\%16=8\text{ or }(i\%16\neq0\text{ and }h\geqslant w)\\\pm j\cdot w/8&\text{otherwise}\end{cases}\)

和(10):

\(\rho_{y,j}=\begin{cases}\pm j\cdot h/8&i\%16=8\text{ or }(i\%16\neq0\text{ and }h\geqslant w)\\0&\mathrm{otherwise},\end{cases}\)

其中 j 是量化偏移 ρ_j 的偏移索引。 (9)和(10)中的ρ_x,j和ρ_y,j的符号表示偏移方向，如果角度索引i < 16，则将其设置为正，否则设置为负。偏移参数量化后，式(6)改写为(11):

\(\begin{aligned}d(x_{\mathrm{c}},y_{\mathrm{c}})&=((x_{\mathrm{c}}+\rho_{x,j})\cdot cosLut[i])\gg3+((y_{\mathrm{c}}+\rho_{y,j})\cdot cosLut[(i+8)\%32])\gg3.\end{aligned}\)

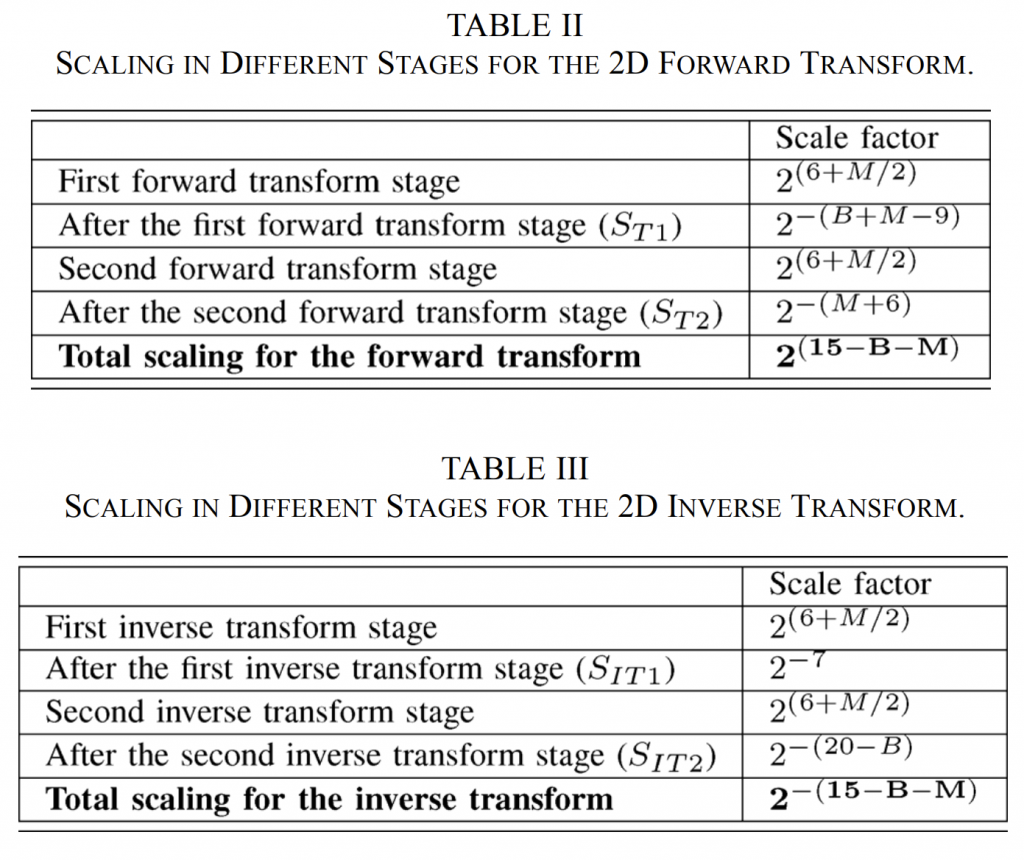
表 II 中列出的几个冗余量化偏移在所提出的 GPM 算法中被删除。因此，GPM 划分模式的总数为 \(N_\mathrm{GPM}~=~N_{\varphi}N_{\rho}~-~N_{\varphi}/2~-~2~-~4~=~64\) ，其中 N_ψ = 20，N_ρ = 4。GPM 划分模式如图 7 所示，按相同的角度索引 i 分组。图 7 中的虚线划分线展示了未包含在所提出的 GPM 设计中的冗余模式。支持的 64 种 GPM 分区模式由语法元素 merge_gpm_partition_idx 进行索引。

4）样本位置的离散化：为了避免GPM预测过程中的额外插值，P0和P1的整数位置在(1)中加权。因此，混合矩阵 W₀ 和 W₁ 需要从基于整数位置的 d(m, n) 导出，其中 m, n ∈ Z ≥0，而不是从 d(x_c, y_c) 导出，其中 x_c, y_c ∈ R。原点转移到图6(d)中的左上角，因为样本位置通常指的是VVC中CU的左上角样本。因此，(11) 的完全离散形式由下式给出(12):

\(d(m,n)=((m+\rho_{x,j})\ll1-w+1)\cdot cosLut[i] +((n+\rho_{y,j})\ll1-h+1)\cdot cosLut[(i+8)\%32]\)

它用于生成混合矩阵 W₀ 和 W₁ 。由于 cosLut[·] 为 3 位精度，且 m 和 n 左移一位，因此 d(m, n) 和 d(x_c, y_c) 的关系满足(13):

\(d(m,n)=\lfloor16d(x_\mathrm{c},y_\mathrm{c})+0.5\rfloor\)

请注意，在 (12) 中，d(m, n) 无需任何乘法即可实现，因为 cosLut[·] 中的值、ρ_x,j 中的 w/8 以及 ρ_y,j中的 h/8 都是基于移位的值。 (12) 的无乘法设计的结果是 GPM 的编码器和解码器复杂度极低。

C. Blending Matrices of GPM

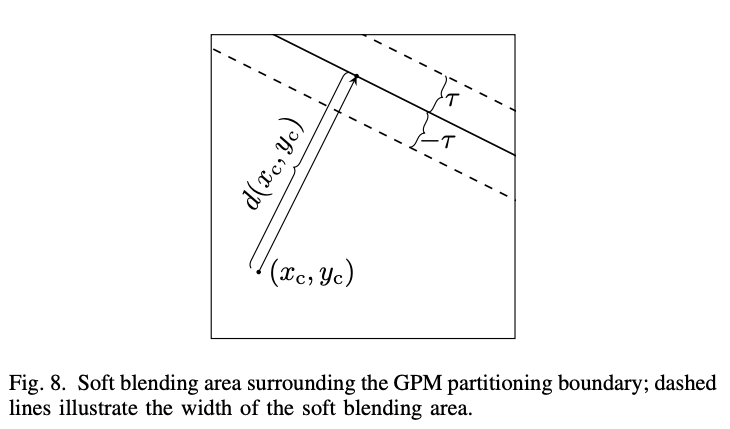
在提出的GPM算法中，应用了软的混合过程。也就是说，如图8所示，当样品位于软混合区域内（即在虚线之间）时，使用(0，8)范围内的加权值倾斜；否则，选择了0或8的完整加权值。一个混合矩阵中单个样品位置的加权值由坡道函数给出(14):

\(\gamma_{x_c,y_c}=\begin{cases}0&d(x_c,y_c)\leqslant-\tau\\\frac{8}{2\tau}(d(x_c,y_c)+\tau)&-\tau<d(x_c,y_c)<\tau\\8&d(x_c,y_c)\geqslant\tau,&\end{cases}\)

τ定义混合区域的宽度。在呈现的GPM算法中，选择τ作为两个样品。基于（13）的τ= 2，(14)被离散为(15):

\(\gamma_{m,n}=\text{Clip}3(0,8,(d(m,n)+32+4)\gg3)\)

其中d(m, n)是根据(12)计算的。然后，可以通过(2)轻松地计算其他混合矩阵的权重。图5可视化一组混合矩阵的示例。请注意，(2)和(15)用于生成Luma分量的混合矩阵，并且基于视频序列的颜色格式，简单地从Luma混合矩阵中进行了色度混合矩阵。

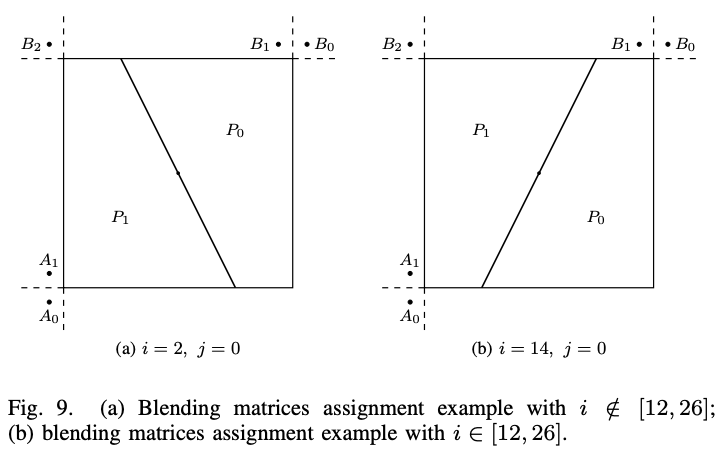
混合矩阵分配基于以下规则：如果角度索引i不在[12，26]的范围内，则将(15)的输出γ_m,n分配给与m∈{0…w – 1}和n∈{0…h – 1}的混合矩阵W0，而W1由(2)计算。否则，如果角度索引i属于[12，26]，则将γ_m,n分配给W1，而w0将推到出。图9显示了解释这些规则的示例。从常规Merge列表中得出的GPM Merge列表是通过在B1，A1，A1，B0，A0和B2的顺序上确定空间相邻CUS的运动信息来构建的。熵编码期间，B1索引的code word通常最短。当预测P0的运动信息由B1预测（即用最短的code word编码）时，GPM中运动信息的信号传输成本被最小化，因为P0的Merge索引在P1 Merge索引之前发出信号。因此，在图9(a)的情况下，\(i\notin[12,26]\)，(15)的γ_m,n分配给W0，而在图9(b)的情况下，γ_m,n分配给W1。

D. Motion Information Storage

在VVC中，使用MCP后使用4×4样品粒度将CU的运动信息存储在缓存中。存储的运动信息用于MV预测和合并列表的构建，或用于推导Deblocking滤波器的边界强度。在VVC的常规MCP中，实际用于预测当前CU的运动信息被跨越并存储到4×4单元中。但是，GPM涉及三种类型的运动信息。也就是说，P0和P1包含其自己的单向MV，而混合区域则通过两者的运动信息进行物理预测。因此，GPM的运动信息存储是基于分区的自适应设计的。

与混合矩阵派生类似，4×4单元的运动存储类型\(T\)由从本机的中心到划分边界的位移d确定。在这里，使用(12)中的4×4单元的整数中心位置计算d，即(4M+2，4n+2)用m∈{0…w – 1}和n∈{0…h – 1}。然后，该4×4单元的运动存储类型\(T\)为(16):

\(T_{4m,4n}=\begin{cases}1-A&d(4m+2,4n+2)\leqslant-32\\2&-32<d(4m+2,4n+2)<32\\A&d(4m+2,4n+2)\geqslant32,&\end{cases}\)

A 表示与混合矩阵对齐对齐的分区分配，由(17):

\(A=\begin{cases}1&i\in[12,26]\\0&otherwise.&\end{cases}\)

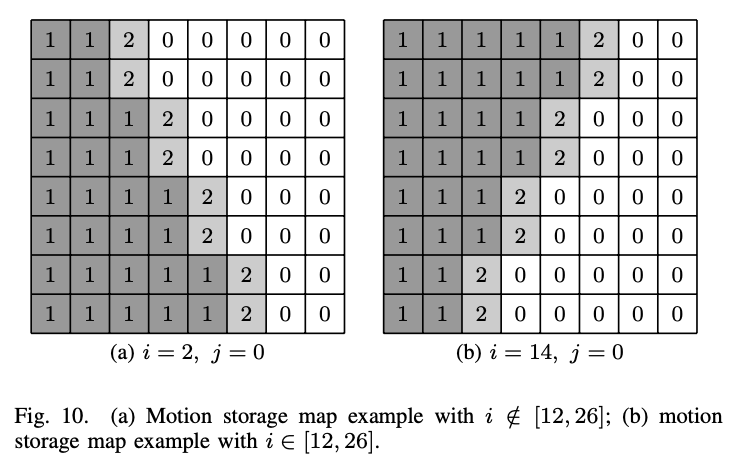
图10显示了具有角度索引\(i\notin[12,26]\)和\(i\in[12,26]\)的GPM运动存储图的示例。 t = 0或t = 1表示相应的4×4单元存储了用于预测P0或P1的单向运动信息，而带有t = 2的单元用于对两个单向运动组合的双向运动信息进行排序。如果P0和P1的运动信息来自同一参考图片列表，则将双向运动信息设置为P1的运动信息。请注意，GPM的运动存储过程通常与硬件实现中的混合过程并行执行，因此，通常在运动存储过程中重新计算d(4M+2, 4n+2)，而不是重复使用d(m, n)来自混合矩阵推导。

E. GPM Merge List Derivation

GPM的运动信息通过Merge模式进行编码。如前所述，GPM的每个部分仅使用单向运动信息，以避免GPM的MCP的其他内存占用。但是，常规Merge列表可能包含直接从相邻CUS复制的单向或双向Merge候选。由于双向Merge候选，常规Merge列表不能直接用作GPM Merge列表。

GPM Merge列表是通过GPM Merge索引的奇偶性从常规Merge列表中派生出来的。也就是说，对于具有GPM Merge索引的偶数值的候选者，使用来自具有对应的常规Merge索引的参考图片列表L0的MV0作为GPM Merge候选者。如果MV0不可用，则使用来自参考图片列表L1的MV1。相反，选择MV1作为GPM Merge索引的奇数值的默认GPM Merge候选，并且如果MV1不可用，则使用MV0。基于索引奇偶校验的方法直接从常规Merge列表中提取GPM Merge候选，而无需修剪，这将实现复杂性降至最低。

表III显示了GPM Merge列表推导的示例。在表III(a)中所示的常规Merge列表的示例中，索引2和3的Merge候选中包含仅可用MV1的单向MV_S，而其他Merge候选可以使用的是双向MV_S。相应的GPM Merge列表如表III(b)所示，MV1用于索引2的候选，因为默认MV0不可用。 GPM Merge候选者的其余部分是根据GPM Merge索引的奇偶校验从常规Merge列表中提取的。

F. Entropy Coding

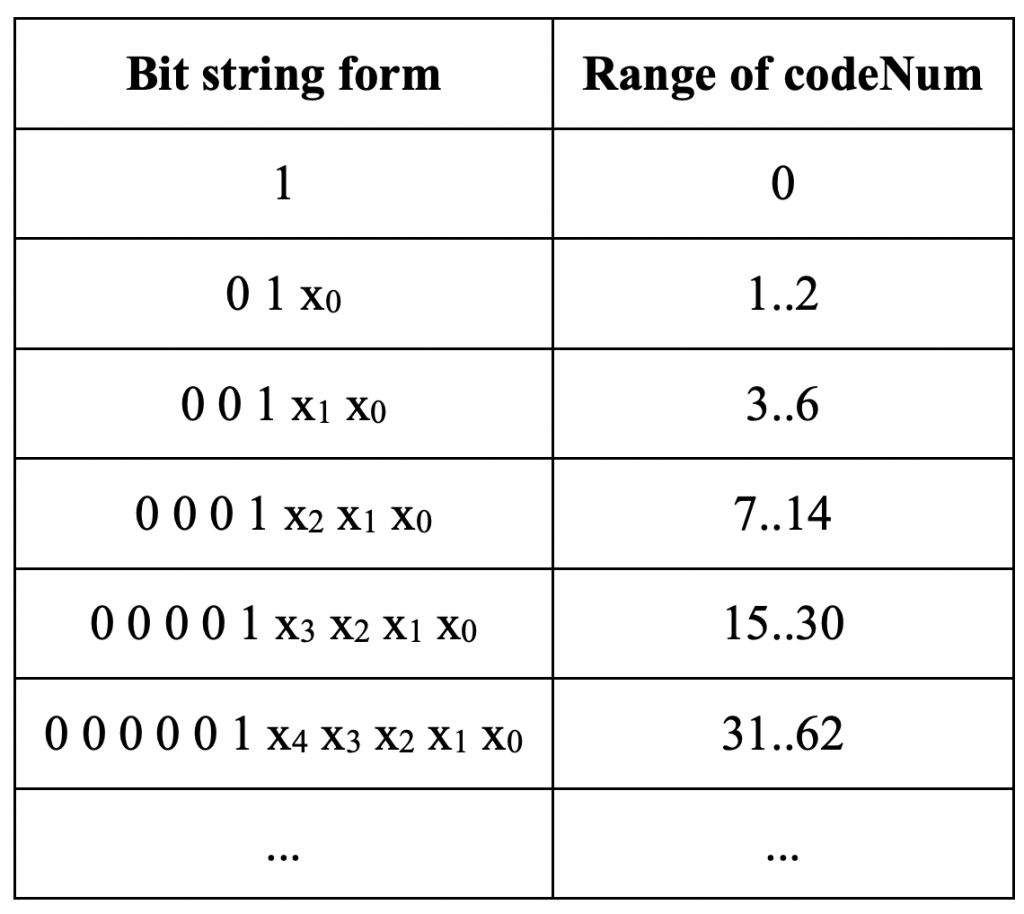
GPM的几个语法元素使用熵编码被编码到位流中。在高级语法HLS中，启用标志的GPM和GPM Merge候选者的最大数量在序列参数集SPS中编码。 GPM启用标志用固定长度代码进行编码，而GPM Merge候选者的最大数量相对于常规Merge候选者的最大数量，并用0-阶指数指数Golomb代码进行编码。

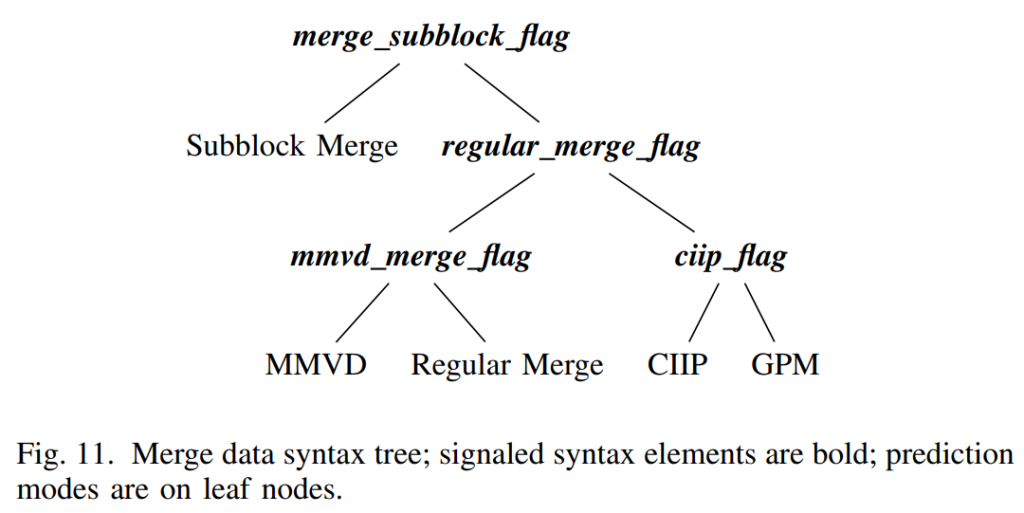
图11示出了Merge数据的语法树。因为 GPM 模式是在Merge数据语法树的底部用信号通知的，所以在 CU 级别不需要 GPM 启用标志。当获取的 ciip 标志为 0 并且满足 GPM 的应用条件时，GPM 隐式启用。

表IV是GPM的部分语法元素表。使用VVC的基于上下文的自适应二进制算术编码（CABAC）引擎对三个语法元素进行编码，包括GPM分区索引（merge_gpm_partition_idx）、P0的Merge索引（merge_gpm_idx0）和P1的Merge索引（merge_gpm_idx1）。由于merge_gpm_partition_idx是大致均匀分布的，因此使用固定长度代码对其进行二进制化，并使用CABAC的旁路模式（无上下文模型）对其进行编码，以简化编码过程，而merge_gpm_idx0和merge_gpm_idx1用0阶截断Rice码进行二进制化，并使用用相同的常规Merge索引初始值初始化的一个单个上下文模型进行编码。注意，所使用的GPM Merge索引GPM_idx_0,1通过以下方式从用信号发送的语法元素导出(18)：

\(\mathrm{GPM\_idx}_0=merge\_gpm\_idx0\)

和(19):

\(\begin{aligned}\text{GPM_idx}_1&=merge\_gpm\_idx1\\&+(merge\_gpm\_idx1\geqslant\text{GPM_idx}_0)?1:0,\end{aligned}\)

因为两个Merge索引不允许相同。

G. Encoder Search

所提出的 GPM 算法中应用了基于率失真优化 (RDO) 的编码器搜索。与基于纹理的搜索方法相比，基于RDO的搜索更容易捕获包含相似纹理的几何分离的运动场。此外，对于不同的视频内容，基于 RDO 的搜索比基于统计的方法更通用。

假设用信号发送的GPM Merge候选的最大数量是六，则每个划分模式总共具有6×5=30个运动信息组合，因为GPM_idx0和GPM_idx1不相同。由于在 GPM 中设计了 N_GPM = 64 划分模式，因此编码器将从 6 × 5 × 64 = 1920 个划分和运动信息的组合 GPM 候选中选择一个。作为比较，在 VTM 7.0 中使用基于完全搜索的 RDO 对多达 6 × 5 × 2 = 60 个组合的 TPM 候选进行了详尽的测试。组合的 GPM 候选者的数量对于 RDO 在编码器侧执行完整的混合和变换编码过程来说非常大。为了降低 GPM 编码器搜索的计算复杂度，使用以下四个阶段确定最佳匹配 GPM 候选者：

Stage1：对于GPM Merge列表的每个单向运动信息候选，执行六个GPM Merge候选上的全CU MCP以获得与当前CU大小相同的六个矩形预测器。预测变量和原始信号之间的亮度分量的绝对差之和 (SAD) 计算为 SAD_CU,k，其中索引 k ∈ {0 … 5}。此阶段排除 GPM Merge候选列表中的相同条目。如果Merge候选列表中的所有运动信息相同，则中止整个GPM编码器搜索。

Stage2：对于每个 GPM 划分模式，使用硬混合矩阵屏蔽掉由六个矩形预测器的 GPM_idx0 预测的部分（即，仅选择 0 或 8 作为权重值，具体取决于位移 d(m, n)的符号.)。计算这些部分的亮度 SAD 并表示为 SAD_P0,k,l，其中 k = 0… 5 且 l = 0…63. 由于使用了硬混合矩阵（无混合区域），因此通过 GPM_idx1 预测的部分的 SAD 可以通过以下方式获得(20):

\(\mathrm{SAD}_{\text{P}1,k,l}=\mathrm{SAD}_{\text{CU},k}-\mathrm{SAD}_{\text{P}0,k,l}.\)

对于索引为 l 的划分模式，组合率失真 (RD) 成本 J_α,β,l 由下式给出(21):

\(J_{\alpha,\beta,l}=\text{SAD}_{\text{P}0,\alpha,l}+\text{SAD}_{\text{P}1,\beta,l}+\lambda(R_\alpha+R_\beta)\)

其中α和β表示预测指标GPM_idx0和GPM_idx1，R_α和R_β表示相应的估计码率。 α 和 β 都属于 {0…5}，但 α = β 的情况被排除在编码器搜索中。 GPM 候选按 J_α,β,l 排序。此外，排除具有 J_α,β,l > SAD_CU,k +λR_k 的 GPM 候选，其中 R_k 是第 k 个 GPM Merge候选的估计码率。

Stage3：第 2 阶段中最好的 60 个（或更少）组合 GPM 候选者用于进行软混合过程，以在亮度分量中生成 P_G。每个组合候选的 GPM 预测器 P_G 和原始信号之间的亮度绝对变换差 (SATD) 之和计算为 SATD_PG,l。 RD 成本更新为(22):

\(\begin{aligned}J’_{\alpha,\beta,l}&=\text{SATD}_{\text{PG},l}+\lambda(R_\alpha+R_\beta+R_l)\end{aligned}\)

其中R_l表示划分索引的估计码率。 GPM 候选者再次按 J’_α,β,l 排序。在此阶段，使用先前测试的编码工具（例如常规Merge或Affine）的最低 SATD 成本来提前终止。

Stage4：第 3 阶段中最好的八个（或更少）候选者的相应色度分量是通过软混合过程生成的。对这些候选应用残差变换编码（如果存在残差）和基于 CABAC 的码率估计，以获得准确的码率成本 R_GPM，其中包括运动码率、划分模式和残差编码。这些候选信号与原始信号之间的三个分量的失真通过平方差之和 (SSD) 来测量，即 SS_DPG,l。最后，总体 RD 成本最低的 GPM 候选者(23)：

\(J_{\alpha,\beta,l}^{\prime\prime}=\mathrm{SSD}_{\mathrm{PG},l}+\lambda R_{\mathrm{GPM}}\)

被选为最终的GPM模式。

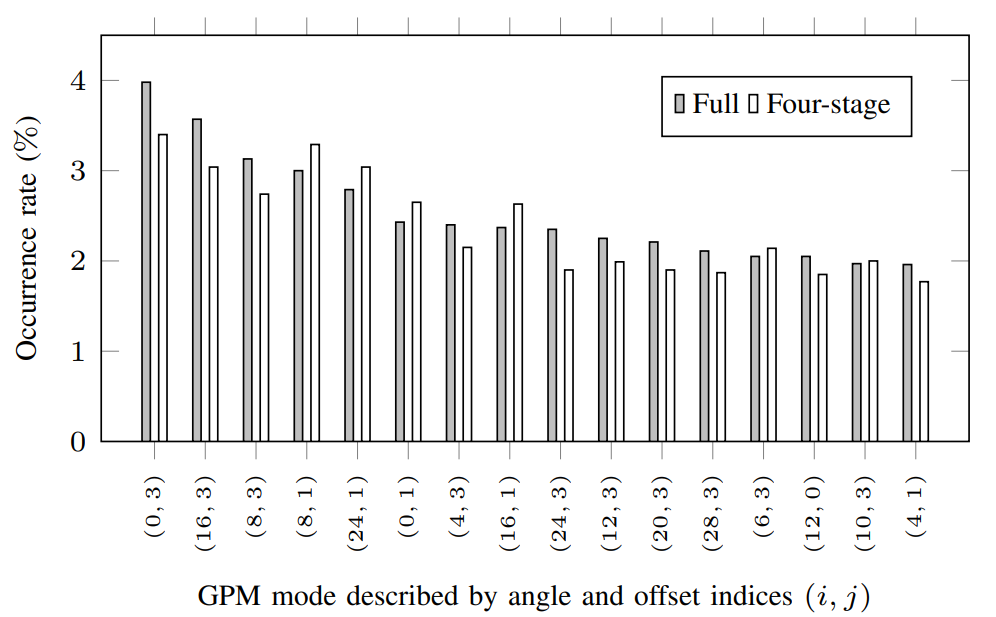
图 12 显示了全搜索中最常用的 16 种 GPM 模式以及这些模式在所提出的四阶段基搜索中的出现率。可以看出，基于四阶段的搜索的发生率趋势与全搜索的发生率趋势相似，这表明基于四阶段的搜索可以以相对较低的编码器复杂度有效地保持编码性能。注意，GPM的编码器搜索算法不限于所提出的基于四阶段的方法。图 12 中呈现的统计数据可以用作其他编码器实现的指南。

VVC中的 Affine motion compensated prediction

在HEVC中，仅应用平移运动模型来进行运动补偿预测（MCP）。在现实世界中，运动有很多种，例如放大/缩小、旋转、透视运动和其他不规则运动。在VVC中，应用基于块的仿射变换运动补偿预测。如图27所示，块的仿射运动场由两个控制点（4参数）或三个控制点运动矢量（6参数）的运动信息来描述。

对于 4 参数仿射运动模型，块中样本位置 (x, y) 处的运动矢量导出为：

对于 6 参数仿射运动模型，块中样本位置 (x, y) 处的运动矢量导出为：

其中，(mv_0x，mv_0y)是左上角控制点的运动矢量，(mv_1x，mv_1y)是右上角控制点运动矢量，以及（mv_2x，mv_2y）是左下角控制点运动矢量。

为了简化运动补偿预测，应用基于块的仿射变换预测。为了导出每个 4×4 亮度子块的运动矢量，根据上述方程计算每个子块的中心样本的运动矢量（如图 28 所示），并四舍五入到 1/16 分数精度。然后应用运动补偿插值滤波器来生成具有导出的运动矢量的每个子块的预测。色度分量的子块大小也设置为4×4。 4×4 色度子块的 MV 计算为对应 8×8 亮度区域中左上和右下亮度子块 MV 的平均值。

与平移运动帧间预测一样，也有两种仿射运动帧间预测模式：仿射Merge模式和仿射 AMVP 模式。

Affine merge prediction

AF_MERGE模式可以应用于宽度和高度都大于或等于8的CU。在该模式下，当前CU的CPMV是基于空间相邻CU的运动信息生成的。最多可以有五个 CPMVP 候选者，并且用信号发送索引来指示要用于当前 CU 的候选者。以下三种类型的 CPMV 候选用于形成仿射合并候选列表：

从相邻 CU 的 CPMV 推断的继承仿射merge候选
使用相邻 CU 的平移 MV 导出的构造仿射merge候选 CPMVP
零 MV

在VVC中，最多有两个继承仿射候选，它们是从相邻块的仿射运动模型导出的，一个来自左相邻CU，一个来自上相邻CU。候选块如图29所示。对于左侧预测器，扫描顺序为A0->A1，对于上面的预测器，扫描顺序为B0->B1->B2。仅选择双方的第一个继承候选人。在两个继承的候选者之间不执行修剪检查。当识别出相邻仿射CU时，其控制点运动矢量用于导出当前CU的仿射merge列表中的CPMVP候选者。如图30所示，若将相邻左下块A采用仿射方式编码，则得到包含块A的CU的左上角、右上角和左下角的运动矢量v₂、v₃和v₄。当块A采用4参数仿射模型编码时，根据v₂、v₃计算当前CU的两个CPMV。如果块A采用6参数仿射模型编码，则根据v₂、v₃和v₄计算当前CU的三个CPMV。

构造仿射候选是指通过组合每个控制点的邻近平移运动信息来构造候选。控制点的运动信息是从图 31 中所示的指定空间邻居和时间邻居导出的。CPMV_k (k=1,2,3,4) 表示第 k 个控制点。对于 CPMV1，检查 B2->B3->A2 块并使用第一个可用块的 MV。对于 CPMV2，检查 B1->B0 块，对于 CPMV3，检查 A1->A0 块。对于 TMVP，如果可用，则用作 CPMV4。

获得四个控制点的 MV 后，基于这些运动信息构建仿射merge候选者。使用以下控制点 MV 组合按顺序构建：

{CPMV1, CPMV2, CPMV3}, {CPMV1, CPMV2, CPMV4}, {CPMV1, CPMV3, CPMV4},
{CPMV2, CPMV3, CPMV4}, { CPMV1, CPMV2}, { CPMV1, CPMV3}

3 个 CPMV 的组合构造了 6 参数仿射合并候选，2 个 CPMV 的组合构造了 4 参数仿射合并候选。为了避免运动缩放过程，如果控制点的参考索引不同，则丢弃控制点MV的相关组合。

在检查继承的仿射合并候选者和构造的仿射合并候选者之后，如果列表仍然未满，则将零个MV插入到列表的末尾。

Affine AMVP prediction

仿射 AMVP 模式可应用于宽度和高度都大于或等于 16 的 CU。在比特流中用信号发送 CU 级别中的仿射标志以指示是否使用仿射 AMVP 模式，然后用信号发送另一个标志以指示是否使用 4 参数仿射或 6 参数仿射。在此模式下，当前 CU 的 CPMV 与其预测器 CPMVP 的差异在比特流中用信号表示。仿射AVMP候选列表大小为2，它是按顺序使用以下四种类型的CPVM候选生成的：

从相邻 CU 的 CPMV 推断的继承仿射 AMVP 候选者
使用相邻 CU 的平移 MV 导出的仿射 AMVP 候选 CPMVP
来自邻近 CU 的平移 MV
零 MV

继承的仿射 AMVP 候选的检查顺序与继承的仿射merge候选的检查顺序相同。唯一的区别在于，对于 AVMP 候选者，仅考虑与当前块中具有相同参考图片的仿射 CU。将继承的仿射运动预测器插入候选列表时，不应用修剪过程。

构造的 AMVP 候选是从图 31 中所示的指定空间邻居导出的。使用与仿射merge候选构造中相同的检查顺序。另外，还检查相邻块的参考图片索引。使用检查顺序中经过帧间编码且具有与当前 CU 中相同的参考图片的第一个块。只有一个当当前CU采用4参数仿射模式编码，并且mv₀和mv₁都可用时，将它们作为一个候选添加到仿射AMVP列表中。当当前CU采用6参数仿射模式编码并且所有三个CPMV都可用时，它们被添加为仿射AMVP列表中的一个候选者。否则，构建的 AMVP 候选者将被设置为不可用。

如果插入有效的继承仿射 AMVP 候选和构造 AMVP 候选后，仿射 AMVP 列表候选仍然小于 2，则将依次添加 mv₀ 、 mv₁ 和 mv₂ 作为平移 MV 来预测当前 CU 的所有控制点 MV，有空的时候。最后，如果仿射AMVP列表仍未满，则使用零MV来填充该列表。

Affine motion information storage

在 VVC 中，仿射 CU 的 CPMV 存储在单独的缓冲区中。存储的CPMV仅用于为最近编码的CU以仿射Merge模式和仿射AMVP模式生成继承的CPMVP。从 CPMV 导出的子块 MV 用于运动补偿、平移 MV 的Merge/AMVP 列表的 MV 导出以及去块。

为了避免附加 CPMV 的图像行缓冲区，来自上面 CTU 的 CU 的仿射运动数据继承与来自正常相邻 CU 的继承的处理方式不同。如果用于仿射运动数据继承的候选CU位于上述CTU行中，则使用行缓冲器中的左下和右下子块MV而不是CPMV来进行仿射MVP推导。这样，CPMV仅存储在本地缓冲区中。如果候选CU是6参数仿射编码，则仿射模型退化为4参数模型。如图 32 所示，沿着顶部 CTU 边界，CU 的左下和右下子块运动向量用于底部 CTU 中 CU 的仿射继承。

HEVC码流中的NALU

翻译自 High Efficiency Video Coding (HEVC) Algorithms and Architectures

HEVC的“high-level syntax”部分包括适用于位流的一个或多个完整Slice或图像的高级信息的信令。例如，高级语法表示视频的空间分辨率，使用了哪些编码工具，并描述了比特流的随机访问功能。除了语法元素的信号外，与语法元素相关的高级工具解码过程也被认为包含在标准的高级语法部分中。示例高级语法解码过程包括参考图片管理和解码图片的输出。

图2.1显示了一个HEVC编码器和解码器。输入图片被送入编码器，编码器将图片编码成比特流。HEVC位流由称为网络抽象层(NAL)单元的数据单元序列组成，每个单元包含一个整数字节。NALU的前两个字节构成NALU头，而NALU的其余部分包含有效载荷数据。一些NALU携带参数集，其中包含应用于一张或多张完整图片的控制信息，而其他NALU携带单个图片中的编码样本。

NALU由解码器解码以产生解码器输出的解码图像。编码器和解码器都将图片存储在已解码的图片缓冲区(DPB)中。这个缓冲区主要用于存储图片，以便以前编码过的图片可以用来生成预测信号，在编码其他图片时使用。这些存储的图片称为参考图片(reference pictures)。

The NAL Unit Header and the HEVC Bitstream

在HEVC中有两类NALU——视频编码层(VCL) NALU和非VCL NALU。每个VCL NALU携带编码图像数据的一个Slice段，而非VCL NALU包含通常与多个编码图像相关的控制信息。一个编码图像，连同与编码图像相关联的非VCL NALU，称为HEVC访问单元（access unit, AU）。没有要求AU必须包含任何非VCL NALU，并且在一些应用程序(如视频会议)中，大多数AU不包含非VCL NALU。但是，由于每个AU都包含一个编码图像，因此它必须由一个或多个VCL NALU组成——编码图像被分割成的每个Slice对应一个单元。

The NAL Unit Header

图2.2显示了NALU Header的结构，它有两个字节长。所有HEVC NALU Header，对于VCL和非VCL NALU，都从这个两字节的NALU头开始，旨在使解析NALU的主要属性变得容易;它是什么类型，以及它属于什么层和时态子层。

NALU报头的第一个位总是设置为’0’，以防止在遗留的MPEG-2系统环境中产生可能被解释为MPEG-2启动代码的位模式。接下来的六位包含NALU的类型，标识NALU中携带的数据类型。6位表示有64种可能的NAL单位类型值。这些值在VCL和非VCL NALU之间平均分配，因此它们各有32种类型。

下面的6位包含一个层标识符，表示NALU属于哪个层，用于将来的可扩展和分层扩展。虽然第一版HEVC于2013年6月发布，支持时间可扩展性，但它不包括任何其他可扩展或分层编码，因此第一版中所有NALU的层标识符(层ID)始终设置为“00000o”。在以后的HEVC版本中，层ID有望用于识别NAL属于哪个空间可扩展层、质量可扩展层或可扩展多视图层。

NALU Header的最后三位包含NALU的时间标识符，表示七个可能的值，其中一个值是禁止的。HEVC中的每个AU都属于一个时间子层，由时间ID表示。由于每个AU属于一个时间子层，所有属于同一AU的VCL NALU在其NALU头中必须具有相同的时间ID。

图2.3显示了编码视频序列中图片的两个不同示例参考结构，两个时态子层都对应于0和1的时态ID值。Slice类型在图中使用I、P和B表示，箭头显示了图片如何参考其他图片。例如，图2.3a中的图B2是使用bi-prediction的图片，参考图片Io和Pl。

VCL NAL Unit Types

表2.1显示了所有32个VCL NALU类型及其NALU类型(图2.2中的NALType)在NAL单元头中的值。所有VCL相同AU的NALU必须具有相同的NALU类型值，该值定义了AU的类型及其编码图。例如，当一个AU的所有VCL NALU的NALU类型都等于21时，则该AU称为CRA AU，编码图像称为CRA图像。在HEVC中有三种基本类型的图像: intra random access point (IRAP) pictures, leading pictures, and trailing pictures.

IRAP Picture

IRAP图像类型由NAL单元类型16-23组成。这包括IDR, CRA和BLA图片类型以及类型22和23，这些类型目前保留供将来使用。所有IRAP图片必须属于时间子层0，并且不使用任何其他图片的内容作为参考数据进行编码(即仅使用intra编码)。注意，但未标记为IRAP的帧内编码图片允许在比特流中出现。IRAP图片类型用于在比特流中提供可能开始解码的点。因此，IRAP图片本身不允许依赖于比特流中的任何其他图片。

比特流的第一张图片必须是IRAP图片，但在整个比特流中可能有许多其他IRAP图片。IRAP图像还提供了切换比特流的可能性，例如当开始观看TV或从一个TV频道切换到另一个频道时。IRAP图片还可以用于在视频内容中实现时间定位——例如，通过使用视频播放器的控制条来移动视频程序中的当前播放位置。最后，IRAP图片还可以、用于在压缩域中从一个视频流无缝切换到另一个视频流。这被称为比特流切换或拼接，它可以发生在两个直播视频流之间，一个直播流和一个存储的视频文件之间，或者两个存储的视频文件之间。从IRAP图像解码并按输出顺序输出任何后续图像始终是可能的，即使按解码顺序在IRAP图像之前的所有图像都从比特流中丢弃。

当为存储和稍后的播放或广播应用程序编码内容时，IRAP图片通常均匀分布，以在整个比特流中提供相似频率的随机接入点。在实时通信应用中，随机访问功能不是那么重要，或者发送IRAP图片所需的相对大量的比特是一个显著的负担，会增加通信延迟，IRAP图片可能很少发送，或者只有当一些反馈信号表明视频数据已经损坏，需要刷新场景时才发送。

Leading and Trailing Pictures

leading picture 是在解码顺序上跟随特定IRAP图并在输出顺序上先于它的图。trailing picture 是在解码顺序和输出顺序上都遵循特定IRAP图片的图片。图2.4展示了leading picture和trailing picture 的例子。在解码顺序上，leading picture和trailing picture 被认为与最接近的IRAP图像相关联，如图2.4中的I1图像。trailing picture必须使用trailing picture NAL单元类型0-5中的一种。特定IRAP图片的trailing picture不允许依赖于任何leading picture或之前IRAP图片的 trailing picture;相反，它们只能依赖于相关的IRAP图片和同一IRAP图片的其他 trailing picture 图片。此外，IRAP图像的所有leading picture必须在解码顺序中位于与同一IRAP图像相关联的所有trailing picture之前。这意味着关联图片的解码顺序总是:(1)IRAP图片，(2)关联的leading picture(如果有)，然后(3)关联的trailing picture(如果有)。

HEVC的trailing picture有三种类型:时间子层访问(TSA)图像、逐级时间子层访问(STSA)图像和普通trailing picture (TRAIL)。

Temporal Sub-layer Access (TSA) Pictures

TSA图像是显示时间子层切换点的trailing picture。TSA图片类型只能用于没有在解码顺序中TSA图片之前的，其时间ID大于或等于TSA图片本身的时间ID，用于预测TSA的图片或用于预测与TSA图片在相同或更高的时间子层中的任何后续(解码顺序)图片。例如，图2.5中的图片P6可以使用TSA图片类型，因为只使用时间子层0中的前一张图片来按照解码顺序预测TSA图片本身和后续图片。

当解码器解码位流中时间子层的子集并且遇到时间子层的TSA图像类型正好在它正在解码的最大时间子层之上时，解码器可以切换到并解码任意数量的附加时间子层。对于图2.5中的示例，仅对TSA 图像的时间子层0进行解码的解码器(1)只解码时域子层0，(2)决定开始解码时域子层1和子层0，或(3)开始解码所有三个子层。对于只转发最低的时间子层的网络节点(例如由于先前的网络拥塞情况)，可能会有类似的动作。网络节点可以检查具有时间ID等于1的传入图片的NAL单元类型。这并不需要大量的计算资源，因为NAL单元类型和时间ID可以在NAL单元头中找到，并且很容易解析。当遇到时序子层1的TSA图像时，网络节点可以切换到按照解码顺序转发继TSA图像之后的任何时序子层图像，而不会存在解码器由于没有所有必要的参考图像而无法正确解码的风险。

Step-wise Temporal Sub-layer Access (STSA) Pictures

STSA图片类型与TSA图片类型类似，但它只保证STSA图片本身以及在解码顺序上与它后面的STSA图片具有相同时间ID的图片不参考在解码顺序上与它前面的STSA图片具有相同时间ID的图片。因此，STSA图像可以用来标记比特流中可以切换到具有与STSA图像相同时间ID的子层的位置，而TSA图像可以标记比特流中可以切换到任何更高子层的位置。图2.5中STSA图的一个例子是图P2。这张图片不可能是TSA图片，因为P3参考了P1。但图片P2可以是STSA图片，因为P6没有参考任何子层1的图片，解码顺序在P2之后的任何子层1的图片也没有参考解码顺序在P2之前的任何子层1的图片。TSA和STSA图片的时间ID都必须大于0。

还要注意的是，由于在HEVC中禁止从较高的时间子层预测到较低的时间子层，因此在任何图片上总是有可能向下切换到较低的时间子层，无论图片类型或时间子层。

Ordinary Trailing (TRAIL) Pictures

普通trailing图片用枚举类型TRAIL表示。trailing图片可以属于任何时间子层。它们可以参考关联的IRAP图片和与同一IRAP图片关联的其他trailing图片，但它们不能参考leading图片(或与同一IRAP图片关联的任何其他非trailing图片的图片)。在按解码顺序输出下一张IRAP图片后，它们也不能输出。请注意，所有TSA和STSA图片都可以标记为TRAIL图片，所有TSA图片都可以标记为STSA图片。然而，为了表明比特流中存在的所有可能的时间子层切换点，建议跟踪图片应使用最具限制性的类型。

Instantaneous Decoding Refresh (IDR) Pictures

IDR图像是一个完全刷新解码过程并开始一个新的CVS的帧内图像。这意味着，无论是IDR图像还是按解码顺序在IDR图像之后的任何图像，都不能依赖于按解码顺序在IDR图像之前的任何图像。IDR图像有两种子类型，IDR_W_RADL类型可能有关联的随机访问可解码leading(RADL)图像，IDR_N_LP类型没有任何leading图像。请注意，即使IDR图片没有任何leading图片，编码器也允许(但不推荐)使用IDR_W_RADL类型。但是，禁止将IDR_N_LP类型用于具有先导图像的IDR。使用两种不同的IDR图片类型的原因是为了使系统层能够在随机访问时知道IDR图片是否是要输出的第一个图片。IDR图像的POC值总是等于零。因此，与IDR图像相关联的leading图像(如果有的话)都具有负的POC值。

Clean Random Access (CRA) Pictures

CRA图片是一个帧内图片，与IDR图片不同，它不会刷新解码器，也不会开始一个新的CVS。这使得CRA图像的leading图像以解码顺序依赖于在CRA图像之前的图像。允许这样的leading图像通常使包含CRA图像的序列比包含IDR图像的序列更具压缩效率(约6%)。

CRA图像的随机访问是通过对CRA图像进行解码，其leading图像在解码顺序上不依赖于CRA图像之前的任何图像，以及在解码和输出顺序上都遵循CRA的所有图像。注意，CRA图片不一定有关联的leading图片。

Random Access Decodable Leading (RADL) and Random Access Skipped Leading (RASL) Pictures

leading图像必须使用RADL或RASL NAL单元类型发出信号。RADL和RASL图片可以属于任何时间子层，但不允许被任何trailing图片引用。RADL图片是保证在对关联的IRAP图片进行随机访问时可解码的leading图片。因此，RADL图片只允许引用关联的IRAP图片和同一IRAP图片的其他RADL图片。

当从关联的IRAP图像执行随机访问时，RASL图像是可能无法解码的先导图像。图2.6显示了两张RASL图片，由于图片P2在解码顺序上位于CRA图片之前，因此这两张图片都是不可解码的。由于其在解码顺序上的位置，在CRA图片的位置随机访问不会解码P2图片，因此无法解码这些RASL图片并将其丢弃。尽管对于可解码的leading图，如图2.6中的RADL图，不禁止使用RASL类型，但为了更加网络友好，建议在可能的情况下使用RADL类型。只有其他RASL图片被允许依赖于一个RASL图片。这意味着依赖于RASL图像的每个图像也必须是RASL图像。RADL和RASL图像可以按解码顺序混合，但不能按输出顺序混合。RASL图片在输出顺序上必须在RADL图片之前。

IDR_W_RADL图片的所有前导图片必须是可解码的，并且使用RADL类型。RASL图片不允许与任何IDR图片相关联。CRA图可能同时具有关联的RADL和RASL图，如图2.6所示。允许RASL图片引用在相关IRAP图片的IRAP图片，也可以参考在解码顺序中遵循该IRAP图片的其他图片，但不能引用解码顺序中更早的图片。图2.6中的RASL图片无法引用图片P0。

在HEVC中有三个约束，目的是在执行随机访问时消除图像输出不均匀。其中两个约束依赖于为每张图片设置的变量PicOutputFlag，它指示图片是否输出。当一个被称为pic_output的标志出现在slice header中并且等于0时，或者当当前图片是RASL图片并且关联的IRAP图片是CVS中的第一张图片时，这个变量被设置为0。否则，PicOutputFlag被设置为1。

第一个约束是，任何具有PicOutputFlag等于1的图片，在解码顺序上位于IRAP图片之前，必须在输出顺序上位于IRAP图片之前。图2.7a中的结构不受此约束，因为图像P1在解码顺序上位于CRA之前，但在输出顺序上位于它之后。如果允许这样做，并且对CRA图片进行随机访问，则会丢失图片P1，导致输出不均匀。

第二个约束是，任何具有PicOutputFlag等于1的图像，在解码顺序上位于IRAP图像之前，必须在输出顺序上位于与IRAP图像相关联的任何RADL图像之前。一个引用结构，即如图2.7b所示，因为P1在I2之前，但在输出顺序上在P3之后。如果允许这种引用结构，并且对CRA图片进行随机访问，则缺少P1图片将导致输出不均匀。

第三个约束是所有RASL图片必须在输出顺序上先于任何RADL图片。由于RASL图片在随机访问时被丢弃，而RADL图片没有被丢弃，因此在RADL图片之后显示的任何RASL图片在随机访问时可能会导致输出不均匀。

其他类型用的比较少，这里就不写了。

Primary Transform in VVC

VVC中的变换设计主要包括三个方面：primary transform, secondary transform and transform partitioning.。 N点变换是指可以应用于N点输入向量的一维变换，这是使用大小为N×N的变换矩阵来完成的。

VVC 继承了 HEVC 变换编码的几个设计方面(参考HEVC Core Transform Design)，包括：1) 使用定点运算，中间数据表示和算术保持为 16 位; 2) 变换过程可以使用直接矩阵乘法或一种快速方法，例如部分蝶形; 3）通过将变换基缩放为 64√N 并通过较小调整舍入到最接近的整数来设计变换内核，其中变换基的范数为 1，N 是变换大小; 4）较小的DCT-2是较大的DCT-2的一部分，因此所有DCT-2内核都嵌入在64×64 DCT-2变换内核中。

尽管在 VVC 中可以应用高达 128 × 128 的编码块大小，但变换编码被设计为与虚拟管道数据单元 (VPDU) 实现兼容。在硬件解码过程中，VPDU是不重叠的64×64块，连续的VPDU由多个管道并行处理。

A. Transform Kernels

在VVC中，除了传统的DCT-2之外，还采用了替代变换类型，包括DST-7和DCT-8。 DST-7和DCT-8的基本函数分别用下面的等式(1)和(2)表示：

其中 N 是变换大小，i = 0, 1,…, N−1 指输出向量的元素索引，j = 0, 1,…, N − 1 指输入向量的元素索引。对于残差的不均匀分布，DST-7 和 DCT-8 通常比 DCT-2 更有效，因为它们的基函数更符合此类统计数据。 DCT-2的大小范围从4点到64点，DST-7/DCT-8的范围从4点到32点。值得注意的是，DST-7 和 DCT-8 的变换基是彼此翻转的版本，具有交替的符号变化。

VVC中定义的变换内核由8位有符号整数组成，HEVC中的所有主要变换内核（包括4点DST-7和从4点到32点的DCT-2）保持不变。 VVC 中定义的附加整数变换内核是通过将浮点变换内核缩放 64√N 得出的，其中 N 是变换大小，并在舍入后进一步调整 ±1。 64点DCT-2的调整是以包含HEVC中定义的所有DCT-2内核、支持部分蝶形并且针对更好的正交性优化内核元素的方式执行的。

对DST-7/DCT-8核进行调整是为了确保与DST-7/DCT-8相关的三个显著特征，如图1所示，包括特征 1）某些基中的重复段{b，f，i，l，o}；2）一个基中的唯一系数值，3）某些基具有固定模式的元组中系数之间的数学关系，保持在具有优化正交性的整数核中。特别地，对于特征3），支持以下公式：

为了将每个系数的 worst-case 乘法与HEVC对齐，对于64点DCT-2和32点DST-7/DCT-8，分别只保留前32个和16个低频系数，并将高频系数归零，这也在最后一个系数位置编码和系数组扫描中考虑。此外，基于DST-7/DCT-8内核的三个特征，VVC中包含了一种支持双重实现的快速变换方案。通过这种方式，快速算法和直接矩阵乘法产生相同的结果。同时，对于16点DST-7/DCT-8，快速方法实现了约50%的乘法运算减少。

在VVC中，primary transform 被指定为可分离变换。支持五种不同的变换类型组合，包括传统的（DCT-2、DCT-2）和四种新的 MTS 模式组合，即（DST-7、DST-7）、（DST-7、DCT-8）、（DCT-8、DST-7）和（DCT-8、DCT-8）。由于有限的编码增益以及引入额外编码器搜索和额外变换组合的复杂性增加，不支持具有额外信令开销的DCT-2和DST-7（或DCT-8）之间的显式组合。在VVC中，DST-7和DCT-8可以应用于多种编码工具中的亮度块，包括多重变换选择（MTS）、帧内子分区（ISP）[34]和子块变换（SBT），这将在下面与变换类型选择相关的小节中详细介绍。对于色度编码，在 VVC 的开发过程中也研究了 DST-7/DCT-8 的潜在优势。然而，由于色度分量通常呈现平滑的纹理，而 DCT-2 就足够了，因此编码增益与复杂性的权衡不太有利。

B. Multiple Transform Selection:

在 VVC 中，MTS有两种变体，称为显式 MTS 和隐式 MTS。显式MTS可以应用于帧内编码块和帧间编码块，而隐式MTS只能用于帧内编码块。在显式MTS中，DST-7/DCT-8的选择由变换类型的显式信令指示。在隐式MTS中，基于编码器和解码器都已知的编码信息来选择变换类型，并且不需要变换类型信令。在序列参数集（SPS）中，有三个控制 MTS 操作的标志。第一个用于启用 MTS 本身。第二个用于在显式或隐式内部 MTS 之间进行选择，最后一个用于启用显式间 MTS。因此，对于后两个标志，如果启用了 MTS，则需要选择四种 MTS 模式组合。在显式MTS中，索引mts_idx在编码单元(CU)级语法的末尾处用信号通知以指示水平变换(trTypeHor)和垂直变换(trTypeVer)的变换类型。 mts_idx的取值范围是0到4，变换类型的映射如表1所示：

MTS索引，表示为mts_idx，仅当亮度块的非零系数存在于DC系数之外并且在左上角的16×16系数区域之外未识别出非零系数时才发出信号，因为DST-7/DCT-8仅对最低的16×16频率系数有影响。换句话说，识别超过最低16×16系数的非零系数意味着不应用DST-7/DCT-8。此外，当启用多个工具时，包括ISP、SBT和低频不可分离变换（LFNST），mts_idx不会发出信号，变换类型推断为DCT-2或预定义的变换类型。在表II中，总结了不同工具的组合，包括MTS、LFNST、MIP、ISP和SBT，其中“Y/N”表示行和列中的相关编码工具可以/不能组合，“N/A”表示相关组合不适用。

隐式 MTS 变换类型是根据编码块的形状导出的。如果块宽度（高度）小于32，则应用DST-7作为水平（垂直）变换。否则，使用DCT-2。同样的规则也用于导出 ISP 编码块的变换。图 2 显示了不同块大小的隐式 MTS 推导示例。 VVC 中的隐式 MTS 设计可以被视为帧内预测残差的 HEVC 变换推导的扩展，通过将 DST-7 的适用块大小从 4 × 4 扩展到 16 × 16（含）以及其间的其他矩形块大小。除了基于块大小的限制之外，仅当 LFNST 和基于矩阵的帧内预测（MIP）索引设置为零时才能应用隐式变换。

隐式 MTS 的优点总结如下： (1) 尽管与显式 MTS 相比，隐式 MTS 提供的编码增益较少，但它在无需任何编码器搜索的情况下提供了比 DCT-2 显着的编码增益。此功能对于无法适应复杂率失真搜索的简单编码器设计很有吸引力。 (2)隐式MTS为ISP编码和非ISP帧内编码块提供统一的变换推导规则。 (3) 由于隐式 MTS 中不允许 DST-7 的维数超过 16，因此避免了对高频系数的内置归零操作（仅适用于 32 点 DST-7）。

HEVC Core Transform Design

翻译自论文 “Core Transform Design in the High Efficiency Video Coding (HEVC) Standard”

A. Use of Transforms in Block-Based Video Coding

在基于块的混合视频编码方法中，变换应用于帧间或帧内预测产生的残差信号，如图 1 所示。在编码器处，帧的残差信号被划分大小为\(N×N\)的方形块，其中\(N=2^M\)和M是一个整数。然后将每个残差块 (\(U\)) 输入到二维\(N×N\)正向变换。通过分别对每行和每列应用\(N\)点一维变换，可以将二维变换实现为可分离变换。然后对得到的变换系数(\(coeff\))进行量化(相当于除以量化步长\(Q_{step}\))以获得量化变换系数(\(level\))。在解码器处，量化的变换系数随后被反量化（这相当于乘以\(Q_{step}\)）。最后，将二维可分离逆变换应用于反量化变换系数(\(coeff_Q\))，从而产生量化样本的残余块，然后将其添加到帧内或帧间预测样本以获得重建块。

通常，正向变换矩阵和逆变换矩阵是彼此转置的，并且被设计为在没有中间量化和去量化步骤的情况下连接时实现输入残差块的近乎无损重建。

在 HEVC 等视频编码标准中，指定了反量化过程和逆变换，而正向变换和量化过程则由实施者选择（受到比特流的约束）。然而，在下文中，除非另有说明，我们将根据正向变换矩阵讨论 HEVC 核心变换的设计和属性。逆变换在HEVC标准中被指定为对应的转置矩阵。

B. Discrete Cosine Transform

应用于输入样本\(u_i\)的\(N\)点 1D DCT 的变换系数\(w_i\)可以表示为:

这里\(i=0,…,N-1\)，\(c_{ij}\)为DCT变换矩阵\(C\)的系数，定义如下：

这里\(i,j=0,…,N-1\), \(A = 1\) or \(2^{1/2}\) for \( i = 0 \) or \(i > 0\)，DCT的基向量\(c_i\)定义为\(c_i=[c_{i0},…,c_{i(N-1)}]^T, i=0,…,N-1\)

DCT 具有多个被认为对于压缩效率和高效实现都有用的属性:

基向量是正交的，即\(c^T_ic_j=0\)。该属性对于通过实现不相关的变换系数来提高压缩效率是理想的。
DCT 的基向量已被证明可以提供良好的能量压缩，这对于压缩效率来说也是理想的。
DCT 的基向量具有相等的范数，即\(c^T_ic_i=1\)。该属性对于简化量化/去量化过程是有利的。假设需要量化误差的相等频率加权，则基向量的相等范数消除了对量化/去量化矩阵的需要。
让\(N=2^M\)。大小为\(2^M×2^M\) DCT 矩阵的元素是 \(2^{(M+1)}×2^{(M+1)}\) DCT 矩阵元素的子集。更具体地，较小矩阵的基向量等于较大矩阵的偶数基向量的前半部分。此属性对于降低实施成本很有用，因为相同的乘法器可以重复用于各种变换大小。
DCT矩阵可以通过使用少量的唯一元素来指定。通过检查 (2) 的元素\(c_{ij}\)，可以看出大小为 \(2^M×2^M\)的 DCT 矩阵中唯一元素的数量等于 \(2^M-1\)。
DCT的偶数基向量是对称的，而奇数基向量是反对称的。此属性对于减少算术运算的数量很有用。
DCT 矩阵的系数具有一定的三角关系，可以减少算术运算的数量，超出利用（反对）对称性质所能实现的数量。

C. Finite Precision DCT Approximations

HEVC 的核心变换矩阵是 DCT 矩阵的有限精度近似。在视频编码标准中使用有限精度的好处是，实值 DCT 矩阵的近似值在标准中指定，而不是依赖于实现。这可以避免制造商使用略有不同的浮点表示实现 IDCT 所导致的编码器-解码器不匹配。另一方面，使用近似矩阵元素的缺点是第 B 节中讨论的 DCT 的一些属性可能不再满足。更具体地说，在与对矩阵元素使用高位深度相关的计算成本和满足第 B 节的一些条件的程度之间存在权衡。

确定 DCT 矩阵元素的整数近似值的一种直接方法是用某个大数（通常在\(2^5\)和\(2^{16}\)之间）缩放每个矩阵元素，然后舍入到最接近的整数。然而，这种方法并不一定能产生最佳的压缩性能。如第 D 节所示，对于给定的矩阵元素位深度，近似 DCT 矩阵元素的不同策略会导致第 B 节的一些属性之间的不同权衡。

D. HEVC Core Transform Design Principles

用于 HEVC 核心变换的 DCT 近似是根据以下原则选择的。首先，B 部分的属性 4、5 和 6 得到满足，没有任何妥协。这种选择确保了 DCT 的几个实现友好的方面得以保留。其次，对于属性 1、2、3 和 7，在用于表示每个矩阵元素的位数和满足每个属性的程度之间存在权衡。

为了测量属性 1、2 和 3 的近似程度，为整数点 DCT 近似定义了以下测量，其缩放矩阵元素等于\(d_{ij}\)，基向量\(d_i=[d_{i0},…,d_{i(N-1)}]^T, i=0,…,N-1\)

正交性度量：\(o_{ij}=d^T_id_j/d^T_0d_0, i≠j\)
与 DCT 的相似性度量：\(m_{ij}=|αc_{ij}-d_{ij}|/d_{00}\)
范数度量：\(n_i=|1-d^T_id_j/d^T_0d_0|\)

比例因子\(α\)定义为 \(d_{00}N^{1/2}\)。

经过仔细研究，决定用8位（包括符号位）来表示每个矩阵系数，并选择第一基向量的元素等于64（即，\(d_{0j}=64\)）。请注意，与正交 DCT 相比，这会导致 HEVC 变换矩阵的比例因子为\(2^{(6+M/2)}\)。其余矩阵元素进行手动调整（在属性 4、5 和 6 的约束内），以实现属性 1、2 和 3 之间的良好平衡。手动调整执行如下。首先，推导出实值缩放 DCT 矩阵元素\(αc_{ij}\) 。

接下来，对于结果矩阵中的每个唯一数字，检查\(αc_{ij}\)区间 [-1.5, 1.5] 周围的每个整数值，并计算 \(o_{ij}\)、 \(m_{ij}\)和 \(n_{ij}\)值。由于变换矩阵中只有 31 个唯一数字（参见第 E 节），因此可以系统地检查各种排列（尽管不是详尽的）。选择最终的整数矩阵元素是为了在所有测量 \(o_{ij}\)、 \(m_{ij}\)和 \(n_{ij}\)之间提供良好的折衷。所得到\(o_{ij}\)、 \(m_{ij}\)和 \(n_{ij}\)的最坏情况值显示在表 I 的第二列中。范数被认为足够接近 1（即范数测量\(n_{ij}\)足够接近 0），以证明不使用非平坦默认值是合理的 HEVC 中的去量化矩阵（即所有变换系数均等缩放）。

为了比较的目的，表I的第三列中列出了将实值DCT矩阵元素与\(2^{(6+M/2)}\)相乘并舍入到最接近的整数时的结果测量。从表中可以看出，虽然HEVC变换的矩阵元素距离缩放后的DCT矩阵元素较远，但它们具有更好的正交性和范数性质。

最后，仅使用 8 位表示，B 节的属性 7（矩阵元素之间的三角关系）不容易保留。作者不知道 HEVC 核心变换的任何三角特性可用于将算术运算数量减少到低于使用（反）对称特性时所需的数量。

E. Basis Vectors of the HEVC Core Transforms

指定32点正向变换的32×32矩阵的左半部分如图2所示。

右半部分可以通过使用基向量的（反）对称性质（B节的性质6）来导出。HEVC的逆变换矩阵被定义为图中矩阵的转置。32×32矩阵包含多达31个唯一数字，如下所示:

这些唯一数字是正向变换矩阵的第一列的元素1至31。请注意，尽管数字90出现了三次，但这是偶然的，通常不是真的。

此外，较小变换矩阵\(N=4,8,16\)的系数可以从 32×32 变换矩阵的系数导出为：

让\(D_4\)表示 4×4 变换矩阵。利用式(4)和图2，\(D_4\)可得：

8×8 变换矩阵和16×16 变换矩阵可以类似地从32×32 变换矩阵获得，如图2所示，其中使用不同的颜色来突出显示嵌入的16×16、8×8 和4×4 正向变换矩阵。此属性允许使用相同的架构来实现不同的变换大小，从而促进不同变换大小之间的硬件共享。

请注意，根据 (3) 的唯一数属性和（反对）对称属性，\(D_4\)也等于：

F. Intermediate Scaling

由于与正交DCT变换相比，HEVC矩阵是按比例\(2^{(6+M/2)}\)缩放的，并且为了通过正向和反向二维变换保持残差块的范数，需要应用额外的比例因子\(S_{T1}\)、\(S_{T2}\)、\(S_{IT1}\)、\(S_{IT2}\)，如图3所示。请注意，图3基本上是图1中变换和量化的定点实现。虽然HEVC标准规定了逆变换的比例因子（即\(S_{IT1}\)、\(S_{IT2}\)），但HEVC参考软件也规定了前向变换的相应比例因子（例如\(S_{T1}\)、\(S_{T2}\)）。比例因子是在以下限制条件下选择的：

所有缩放因子应为 2 的幂，以允许缩放以右移的方式实现。
假设输入残差块的全范围（例如，所有样本都具有最大幅度的DC块），每个变换阶段之后的位深度应等于16位（包括符号位）。这被认为是准确性和实施成本之间的合理权衡。
由于HEVC矩阵按比例\(2^{(6+M/2)}\)缩放，2D正向变换和逆变换的级联将导致1D行正向变换、1D列正向变换、1D列逆变换和1D行逆变换中的每一个的按比例\(2^{(6+M/2)}\)缩放。因此，为了通过二维正变换和逆变换保持范数，所有比例因子的乘积应等于\((1/2^{(6+M/2)})^4=2^{-24}2^{-2M}\)。

图4以4×4正向变换为例说明了选择正向变换比例因子的过程。当视频具有B bit位深度时，残差将在需要(B+1)位来表示的范围\([-2^B+1,2^B-1]\)内。在下面的worst case 位深度分析中，我们将假设残差块的所有样本的最大振幅等于正向变换第一阶段的输入。我们相信这是一个合理的假设，因为所有基向量都具有几乎相同的范数。

还要注意，在worst case 分析中，我们使用\(-2^B\)而不是\(-2^B+1\)或\(2^B-1\)，因为它是2的幂。由于所有比例因子都是2的幂，所以假设输入为\(-2^B\)（仍然适合(B+1)位），则比例因子推导变得更简单。对于这种worst case的输入块，输出样本的最大值将为\(-2^B×N×64\)。这对应于第一基向量（长度为N，所有值均等于64）与由等于\(-2^B\)的值组成的输入向量的点积。因此，对于\(N=2^M\)，为了使输出适合于16位（即，\(2^{-15}\)的最大值）内，需要\(1/(2^B×2^M×2^6×2^{-15})\)的缩放。因此，第一变换阶段之后的比例因子被选择为\(S_{T1}=2^{-(B+M-9)}\)。

正向变换的第二阶段由第一变换阶段的结果与\(D^T_4\)相乘组成。正向变换第二阶段的输入是第一阶段的输出，该输出是一个矩阵，第一行中的所有元素都具有 \(2^{-15}\)的值。所有其他元素将为零，如图 4(b) 所示。与\(D^T_4\)相乘的输出将是一个矩阵，其中仅 DC 值等于 \(2^M×2^6×2^{-15}\)，所有其余值等于 0。这意味着第二阶段变换后所需的缩放为 \(S_{T2}=2^{-(M+6)}\)，以便输出适合 16 位。

逆变换的第一阶段由正变换的结果与\(D^T_4\)相乘组成。逆变换第一阶段的输入是正变换的输出矩阵，该矩阵是仅 DC 元素等于\(2^{-15}\)的矩阵。与\(D^T_4\)相乘的输出将是一个矩阵，其第一列元素等于 \(2^6×2^{-15}\)。因此，在逆变换的第一阶段之后，为了使输出适合 16 位，所需的缩放是\(S_{IT1}=2^{-6}\)。

逆变换的第二阶段包括将逆变换的第一阶段的结果与\(D_4\)相乘。逆变换第二级的输入是逆变换第一级的输出矩阵，该矩阵的第一列元素等于\(2^{-15}\)。与\(D_4\)相乘的输出将是所有元素等于\(2^6×2^{-15}\)的矩阵。因此，在第二阶段逆变换之后，为了使输出值进入 \([-2^B,2^B-1]\)的原始范围所需的缩放是 \(S_{IT1}=2^{-21-B}\)。

总之，本节中施加的约束会在不同的变换阶段后产生以下比例因子：

在第一个正向变换阶段之后：\(S_{T1}=2^{-(B+M-9)}\)
在第二个正向变换阶段之后：\(S_{T2}=2^{-(M+6)}\)
在第一个逆变换阶段之后：\(S_{IT1}=2^{-6}\)
在第二个逆变换阶段之后：\(S_{IT1}=2^{-21-B}\)
其中B是输入/输出信号的位深度（例如 8 位），是\(M=log2(N)\)。

在没有量化/去量化的情况下，比例因子的这种选择可确保在所有变换阶段之后的位深度为 16 位。然而，量化/反量化过程引入的量化误差可能会将每个逆变换阶段之前的动态范围增加到超过 16 位。例如，考虑 B = 8 和正向变换的所有输入样本等于 255 的情况。在这种情况下，正向变换的输出将是值等于 \(255<<7 =32640\) 的 DC 系数。对于高 QP 值并使用向上舍入量化器，每个逆变换级的输入很容易超出 [-32768, 32767] 允许的 16 位动态范围。虽然在去量化器之后clip到 16 位范围被认为是微不足道的，但在第一个逆变换阶段之后被认为是不受欢迎的。为了允许一定程度的量化误差，同时将两个逆变换级之间的动态范围限制为 16 位，逆变换比例因子的选择最终修改如下：

在第一个逆变换阶段之后：\(S_{IT1}=2^{-7}\)
在第二个逆变换阶段之后：\(S_{IT1}=2^{-20-B}\)

逆变换比例因子的使用如图 5 所示，以 4×4 逆变换为例，假设输入是图 4 的最终输出。

表 II 和表 III 分别总结了与正交 DCT 相比正向变换和反向变换的不同缩放因子。

HEVC规范指定在缩放之前添加的偏移值以进行舍入。该偏移值等于比例因子除以 2。图 3-5 中未明确显示该偏移。

最后，使用 8 位系数并将中间数据的位深度限制为 16 位的两个有用结果是，所有乘法都可以用具有 16 位或更少的乘法器来表示，并且右移之前的累加器可以用更少的位来实现。所有变换阶段都超过 32 位。

G. Quantization and De-Quantization

量化由除以量化步长(\(Q_{step}\))组成，逆量化由乘以量化步长组成。类似于H.264/AVC，量化参数(QP)用于确定HEVC中的量化步长。可以取从0到51的52个值。1的增加意味着量化步长增加了大约12%（即\(2^{1/6}\)）。增加6导致量化步长增加2倍。除了指定两个连续QP值的步长之间的相对差之外，还需要定义与QP值的范围相关联的绝对步长。这是通过为\(Q_{step}=1\)选择QP=4来完成的。

正交变换的等效量化步长之间的结果关系现在由下式给出：